2026共通テスト数学ⅡＢＣ解説

2026大学入学共通テスト数学ⅡＢＣの解説を速報します！数学ⅠＡについては↓の記事をご覧くださいm(_ _)m

第１問（必答問題15点）

解答

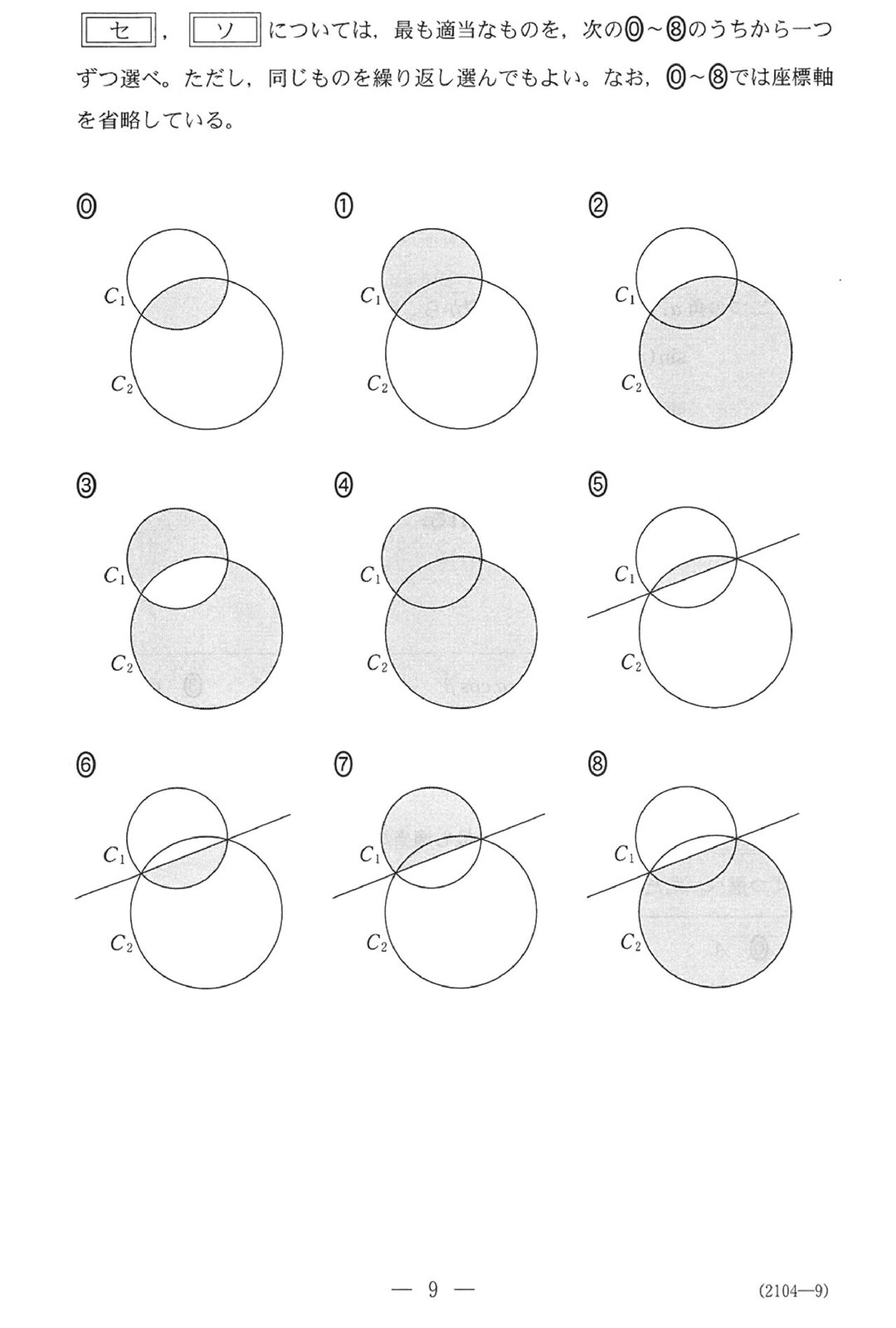
第２問（必答問題15点）

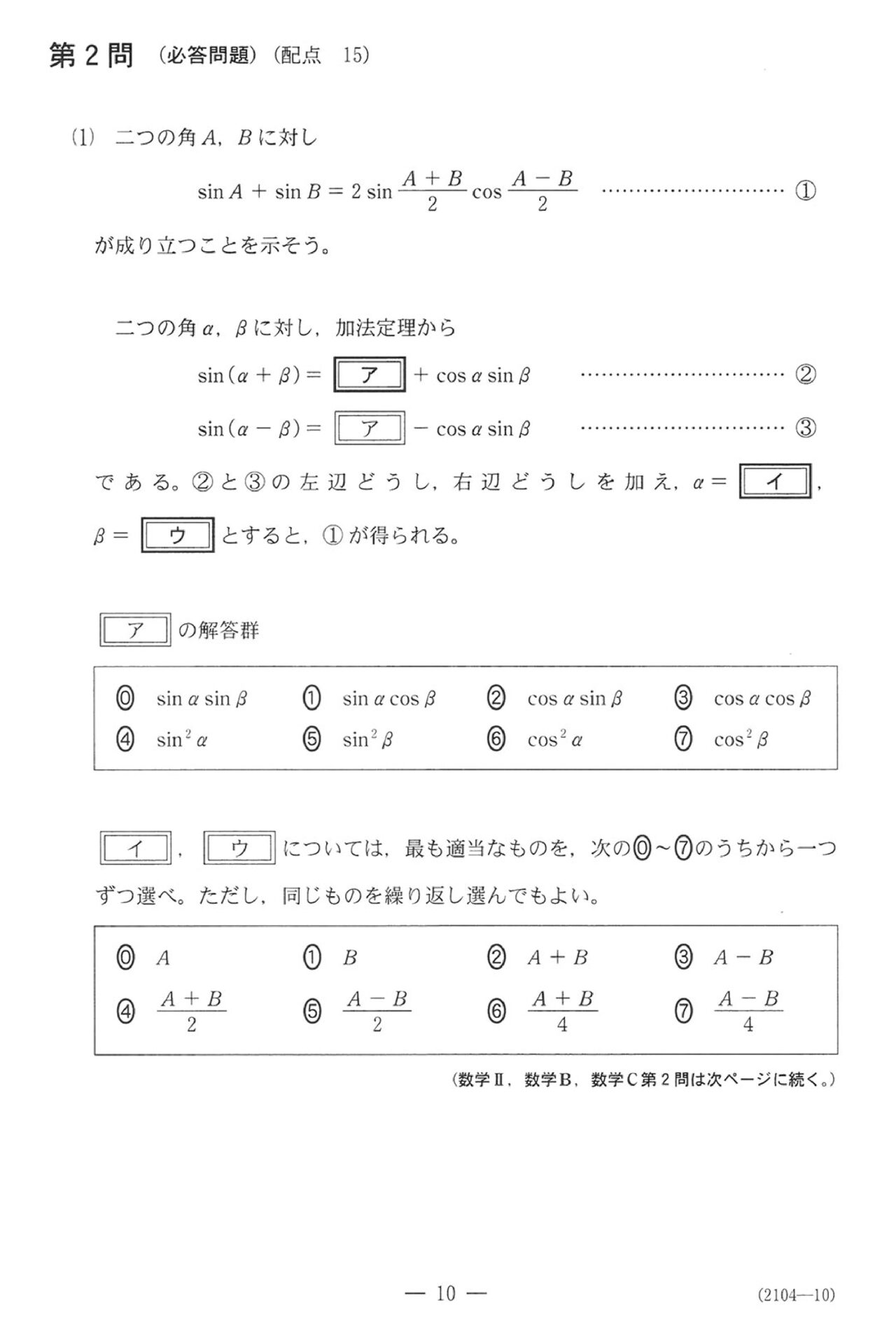
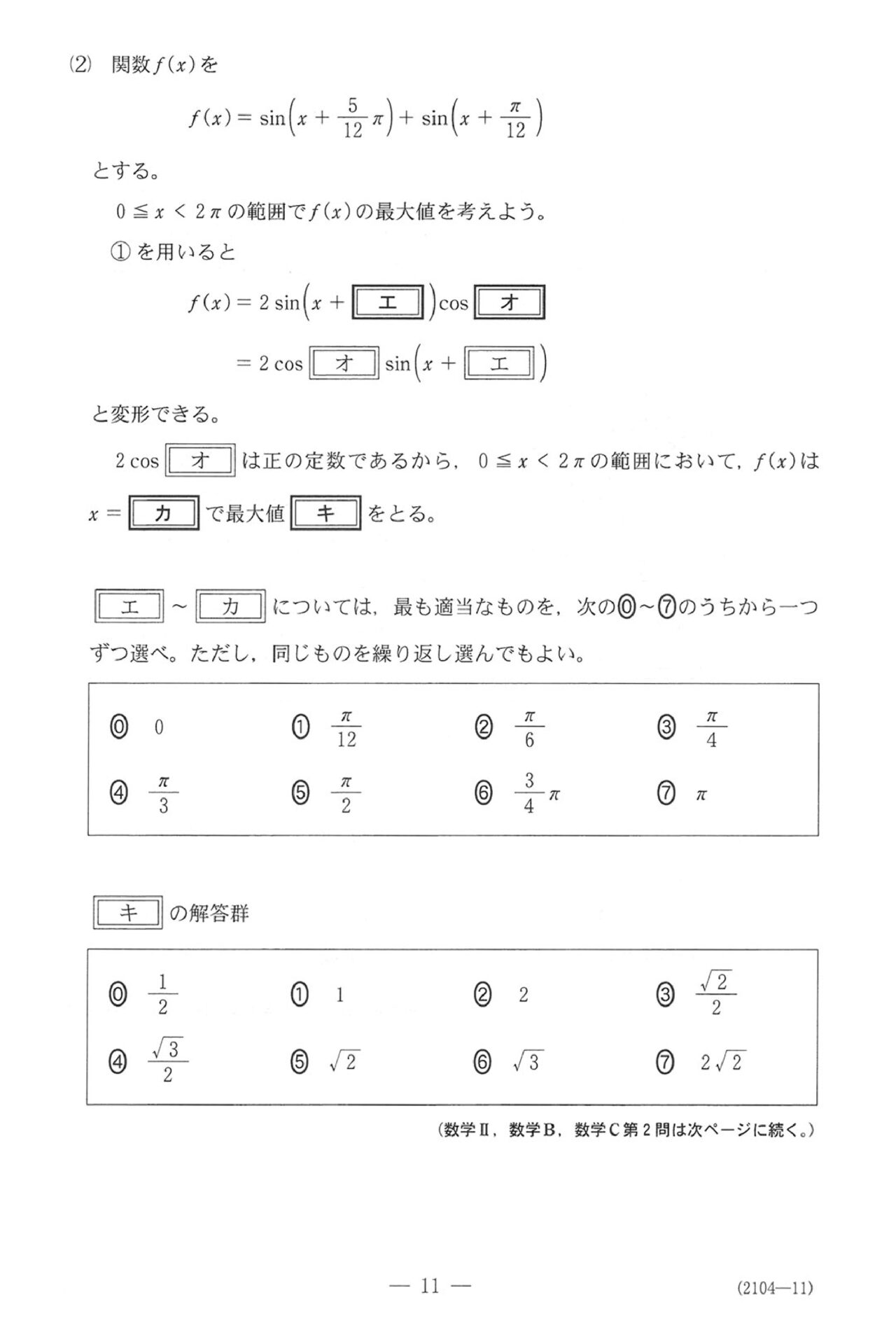
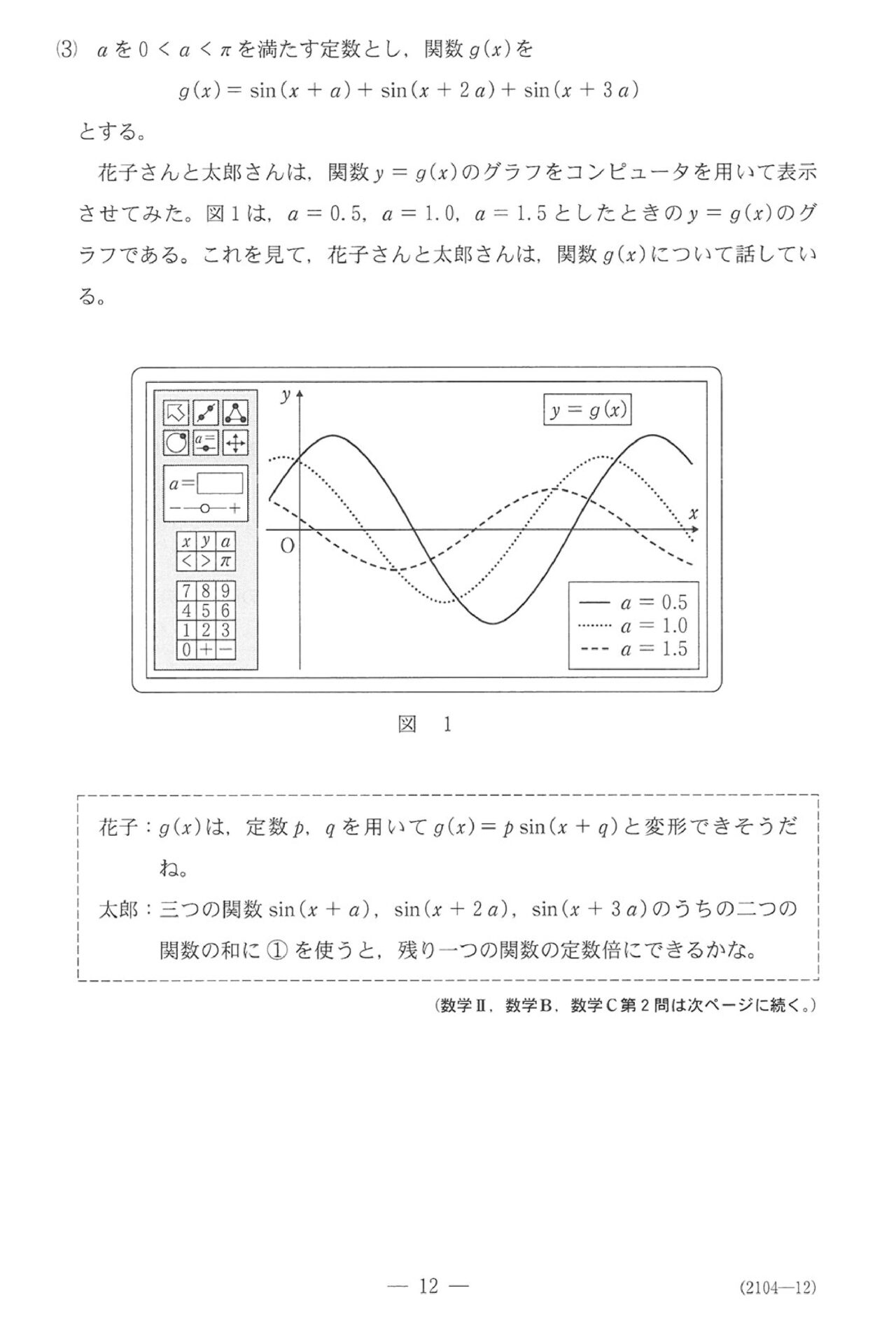
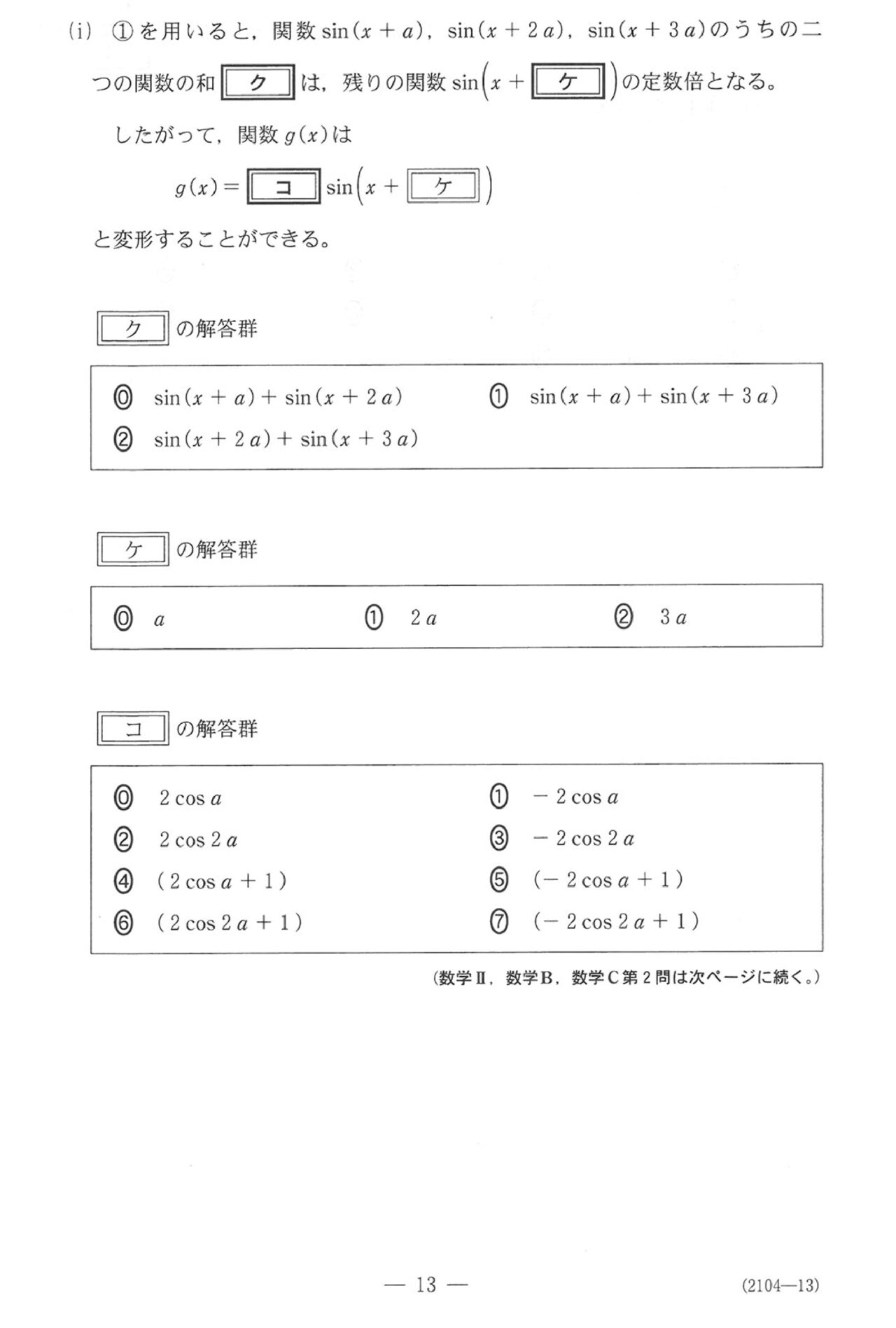
解答

第３問（必答問題22点）

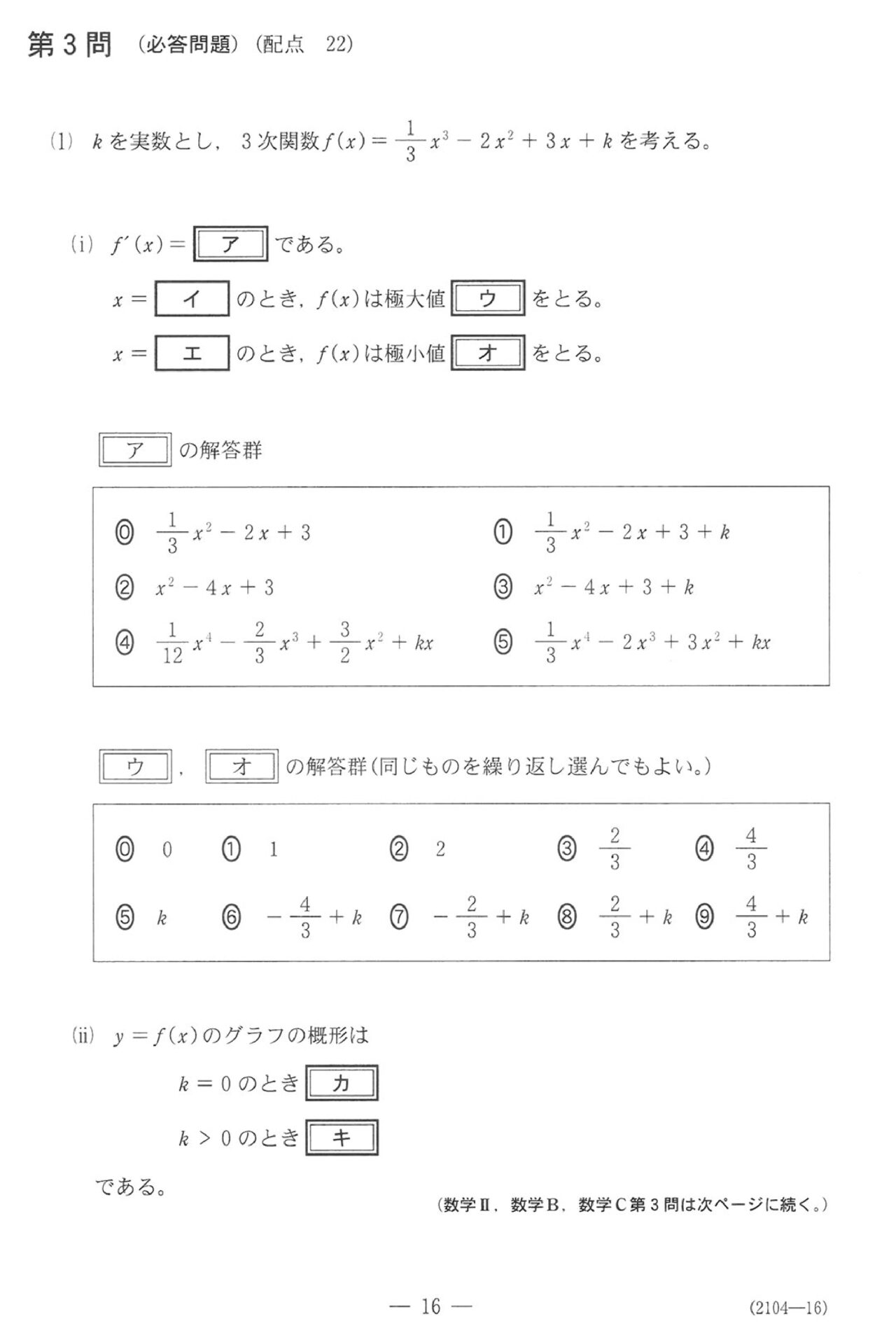
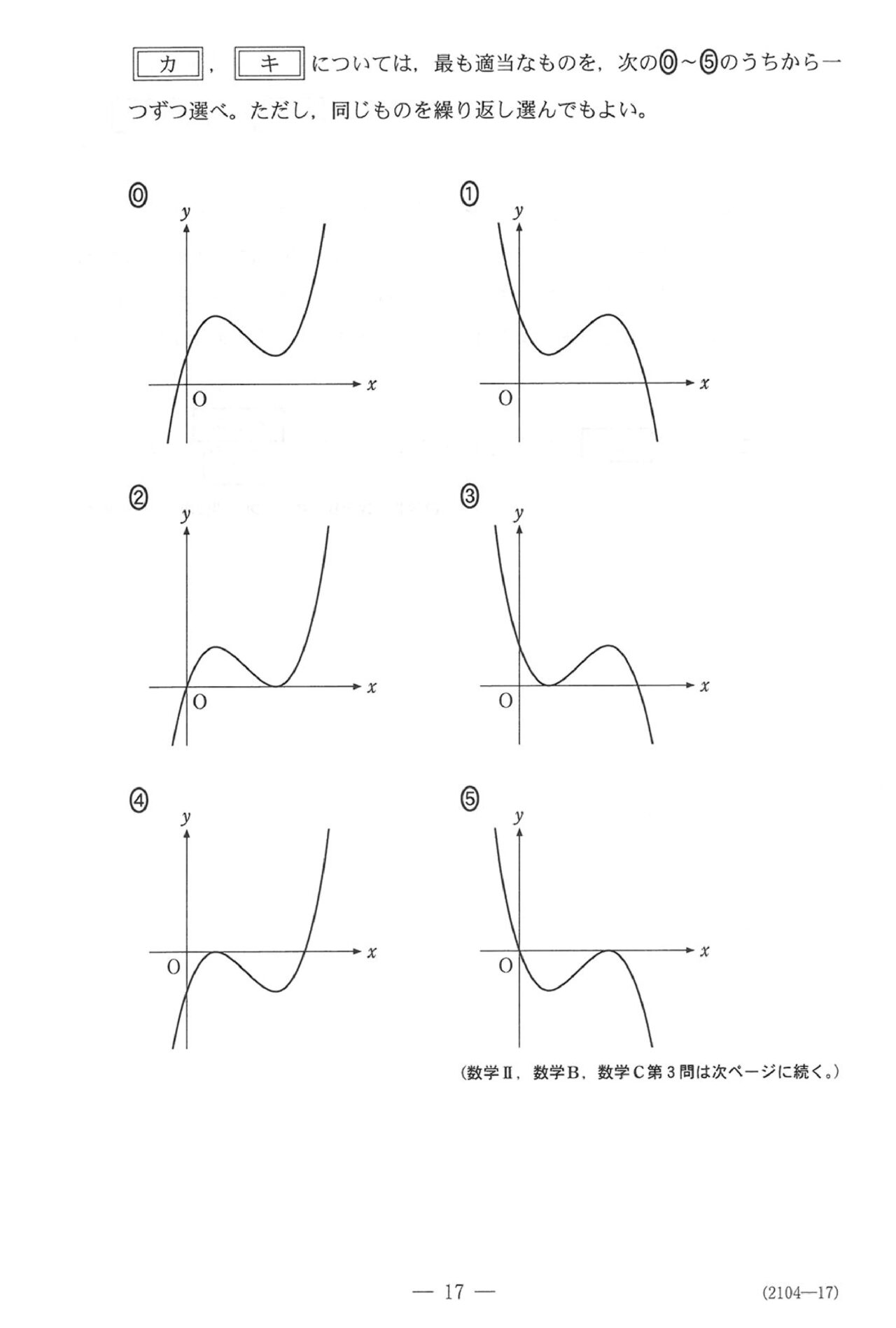
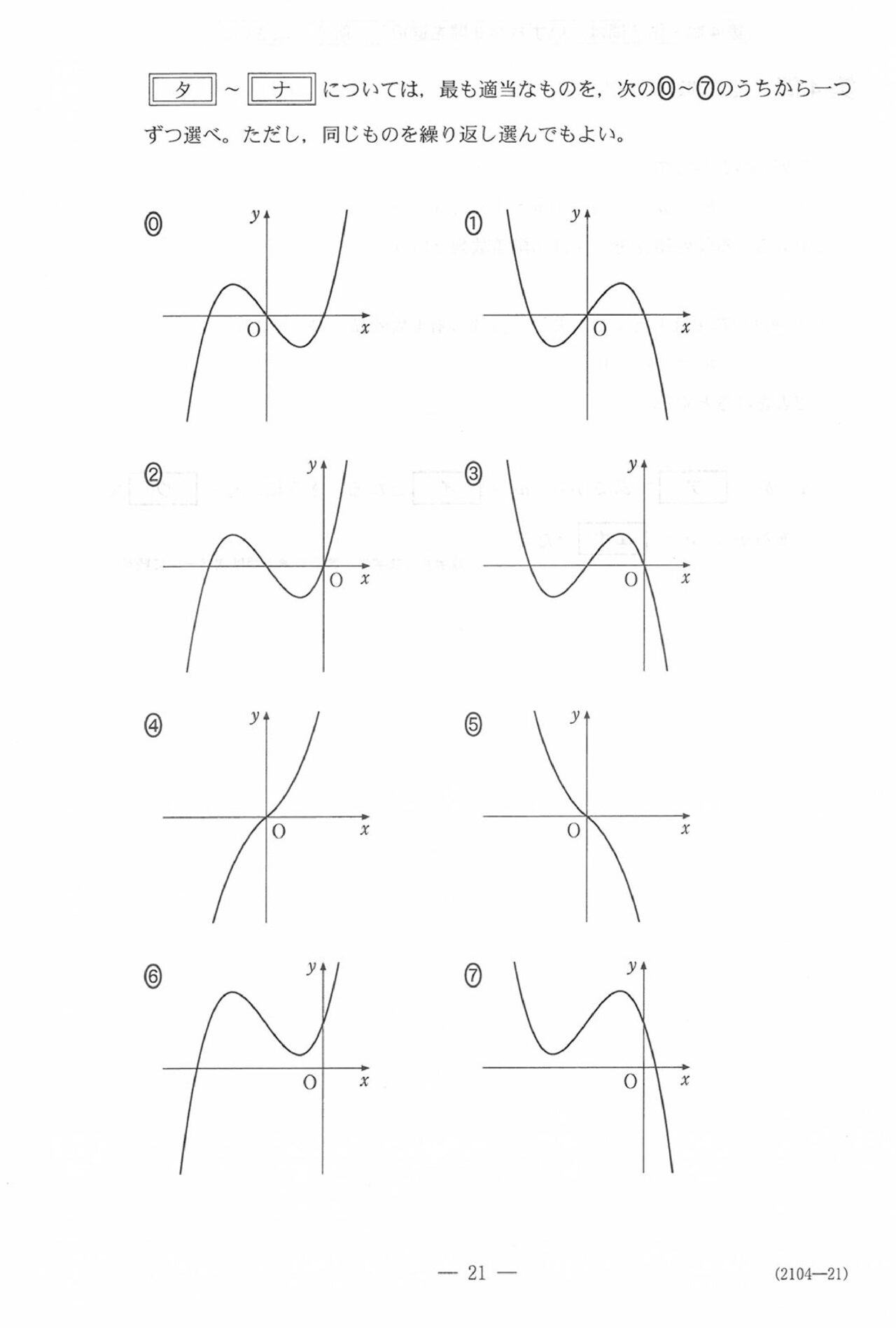
解答

第４問（選択問題16点）

解答

第５問（選択問題16点）

解答

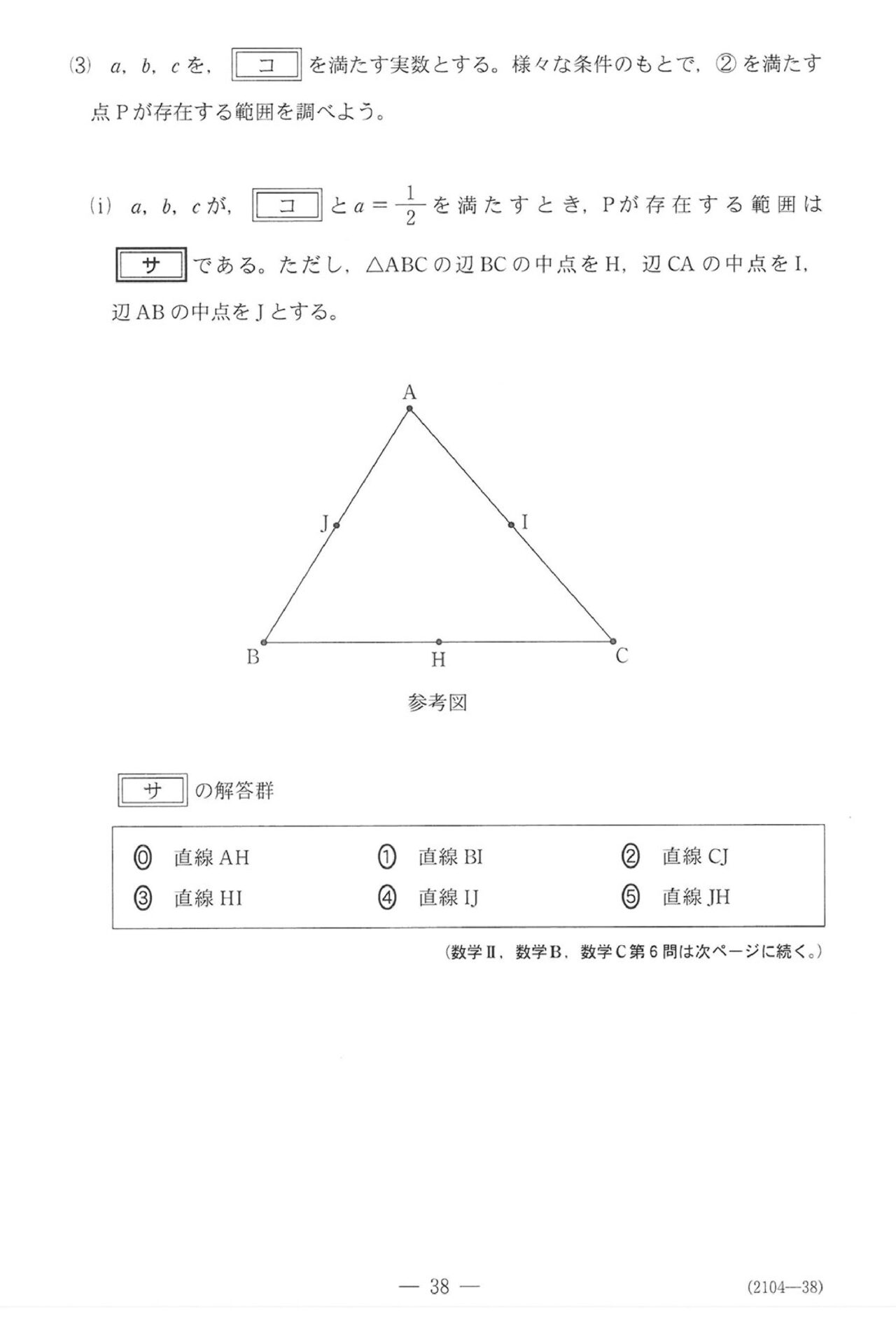
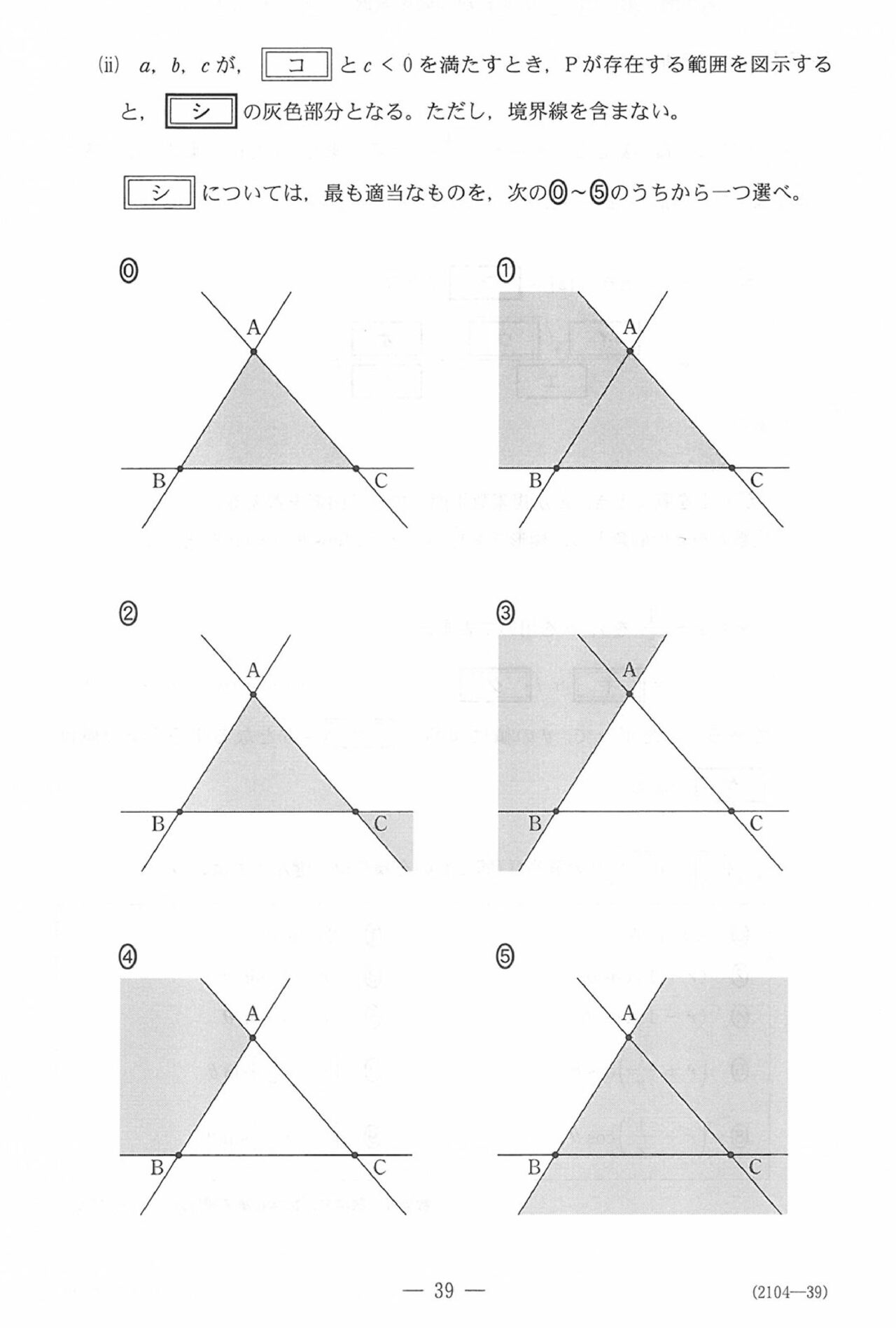
第６問（選択問題16点）

解答

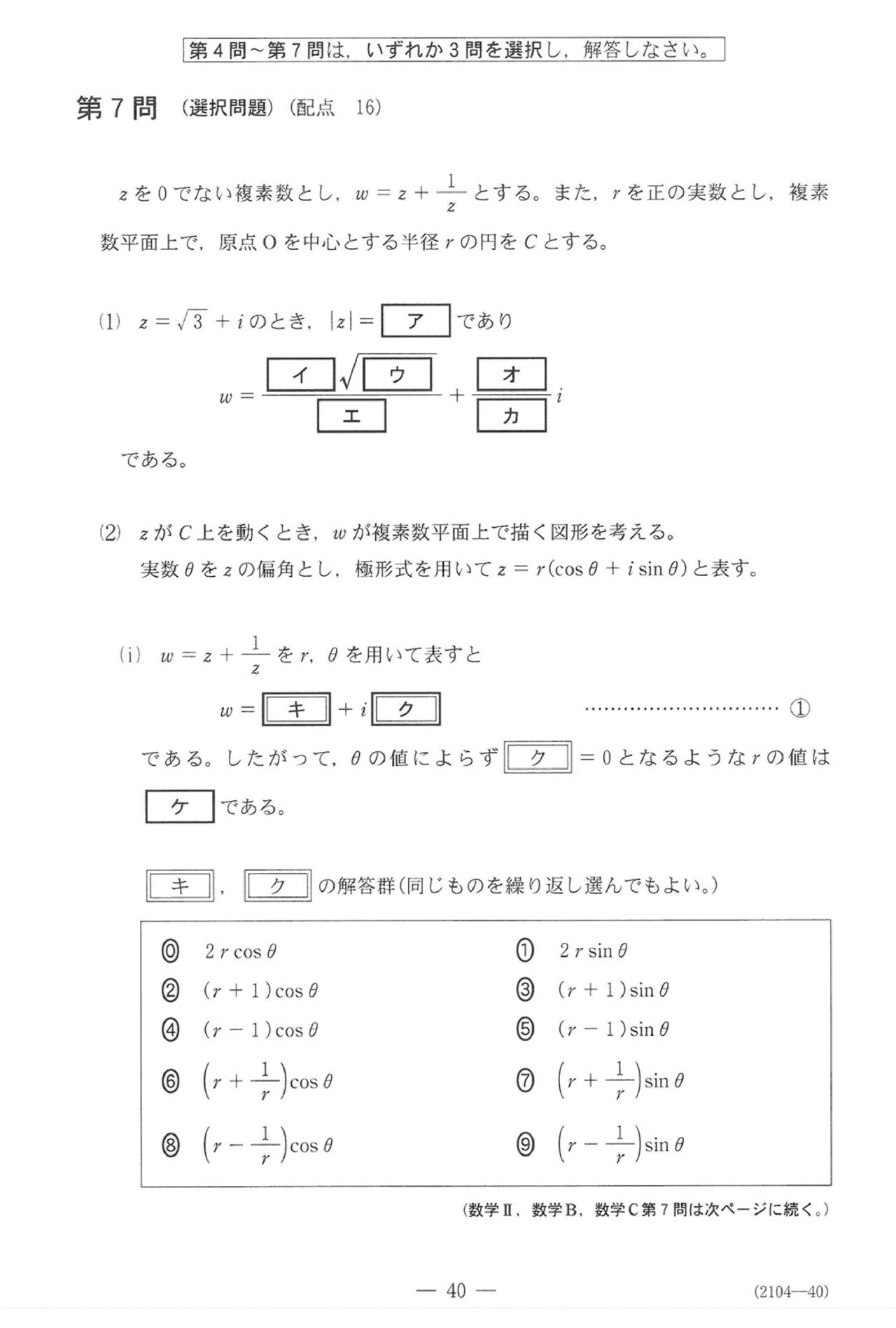
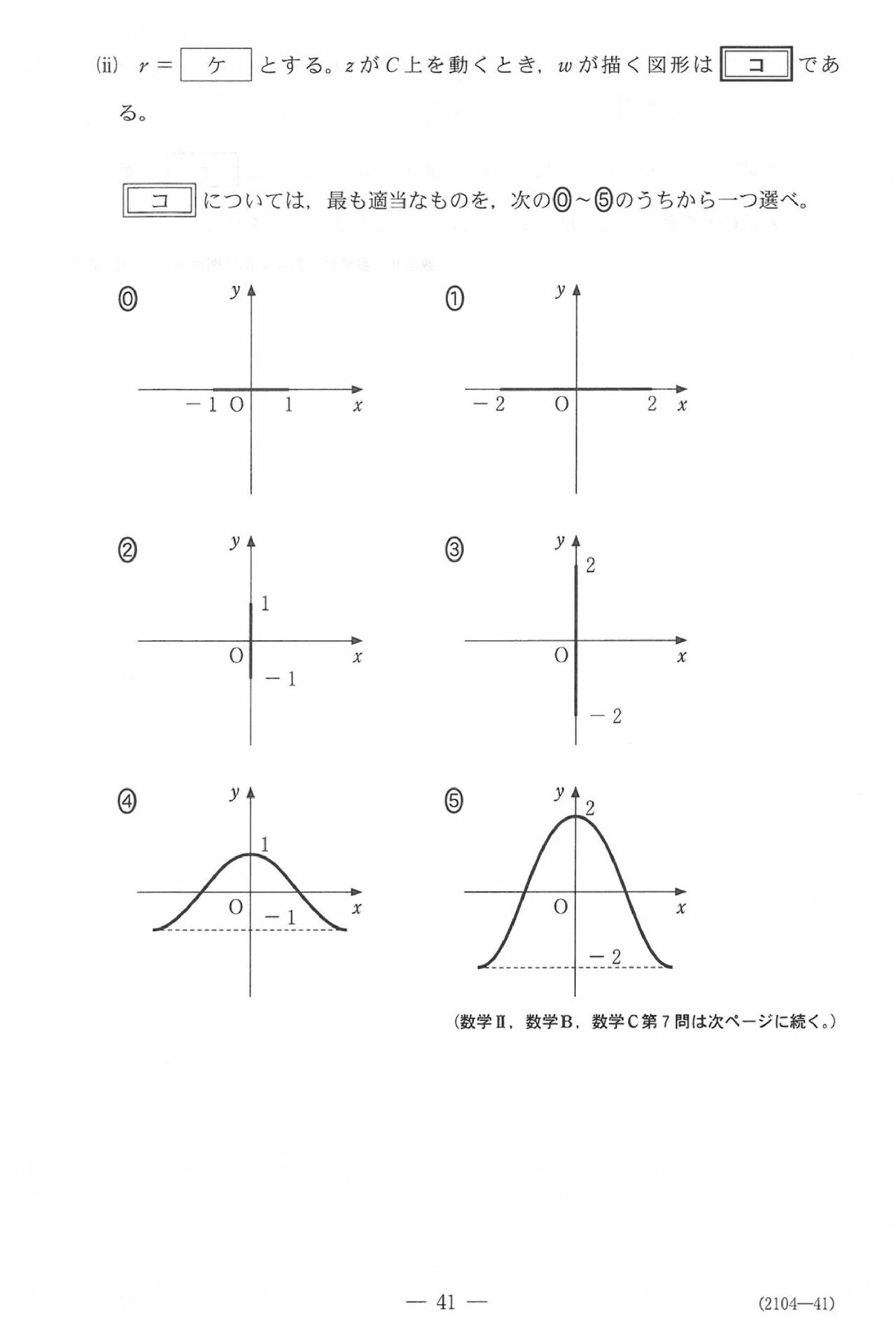
第７問（選択問題16点）

解答

講評

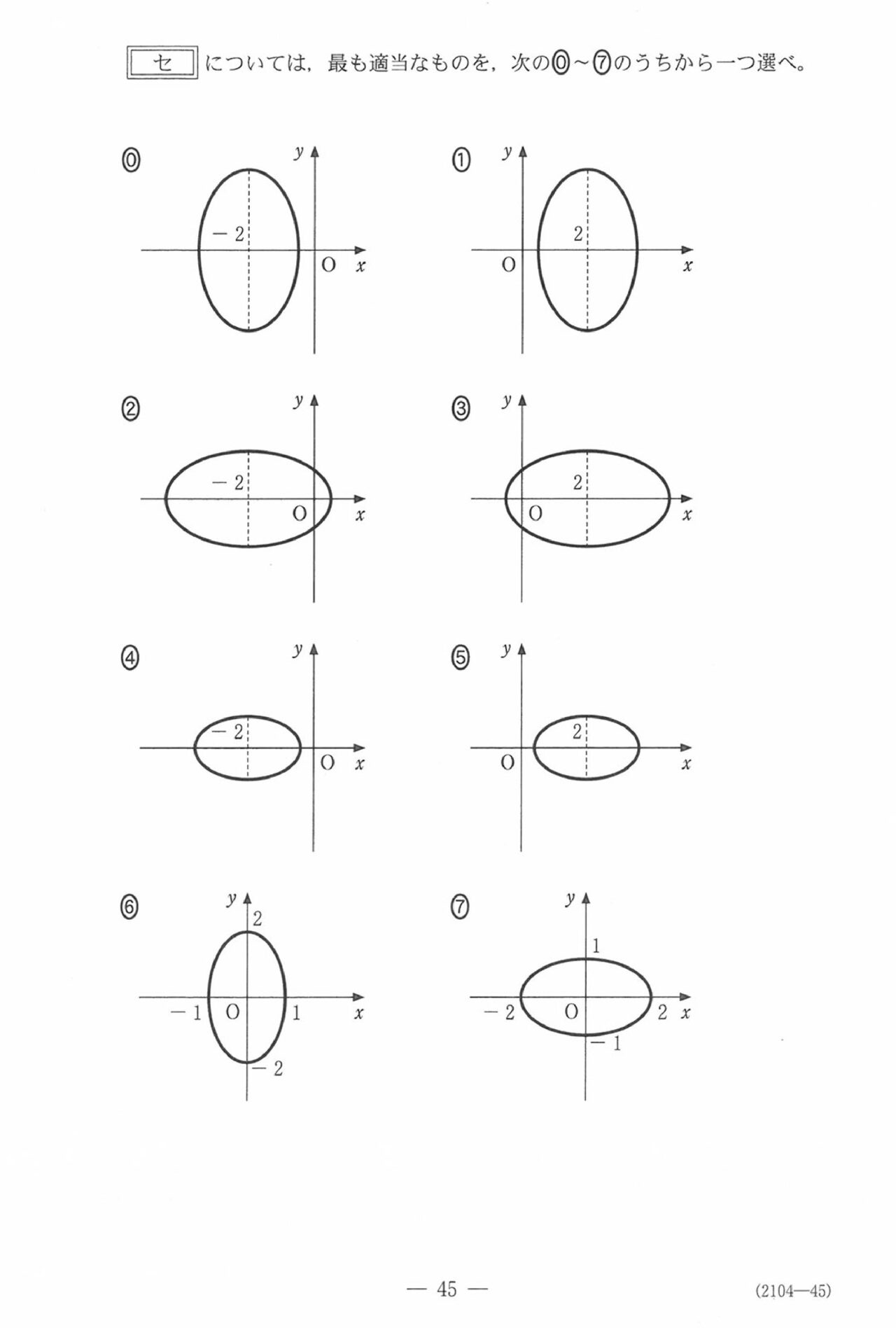
解答方式	試験時間	大問数	難易度
マーク式	70分	６問 （第４～７問は、３問を選択して解答）	変化なし

だと思います。昨年2025と同じく凄いカンタンでした。打ち込む前に時間内で解きましたが…

深夜３時から始めて…

和積公式で３回計算ミスって…

数列の最後で１回計算ミスって…

では、

文系？理系？	選択問題のセレクト
文系生徒	第４・５・６問を解くしかない
理系生徒	第４・６・７問を解くのがオススメ

と指導しているんですが、正直理系生徒でもどれをセレクトしても大差なかったと思います。

第１問

2026の共テ模試は、どこも結構2025の本試から構成をいじってたんですが、それと同様になりました。

でもネタ的には円と領域の問題でカンタンです。共通弦の誘導ついてるんですが、僕は再前半で共通弦を意識して解いちゃったので、解答もそんな感じでいかせて頂いてます。

第２問

ここで三角関数、2023のⅡＢでも出てた和積公式がメインの内容です。

僕は疲れてたんで最後３回計算ミスしたんですが…

君らは若いから１回で当てましょう(笑)

第３問

グラフと求積。全体的に読み取りがメインで、計算は等積条件のとこぐらいです。誘導ついてますが、定積分を２つ計算せず、１つに結合してから計算しましょう。

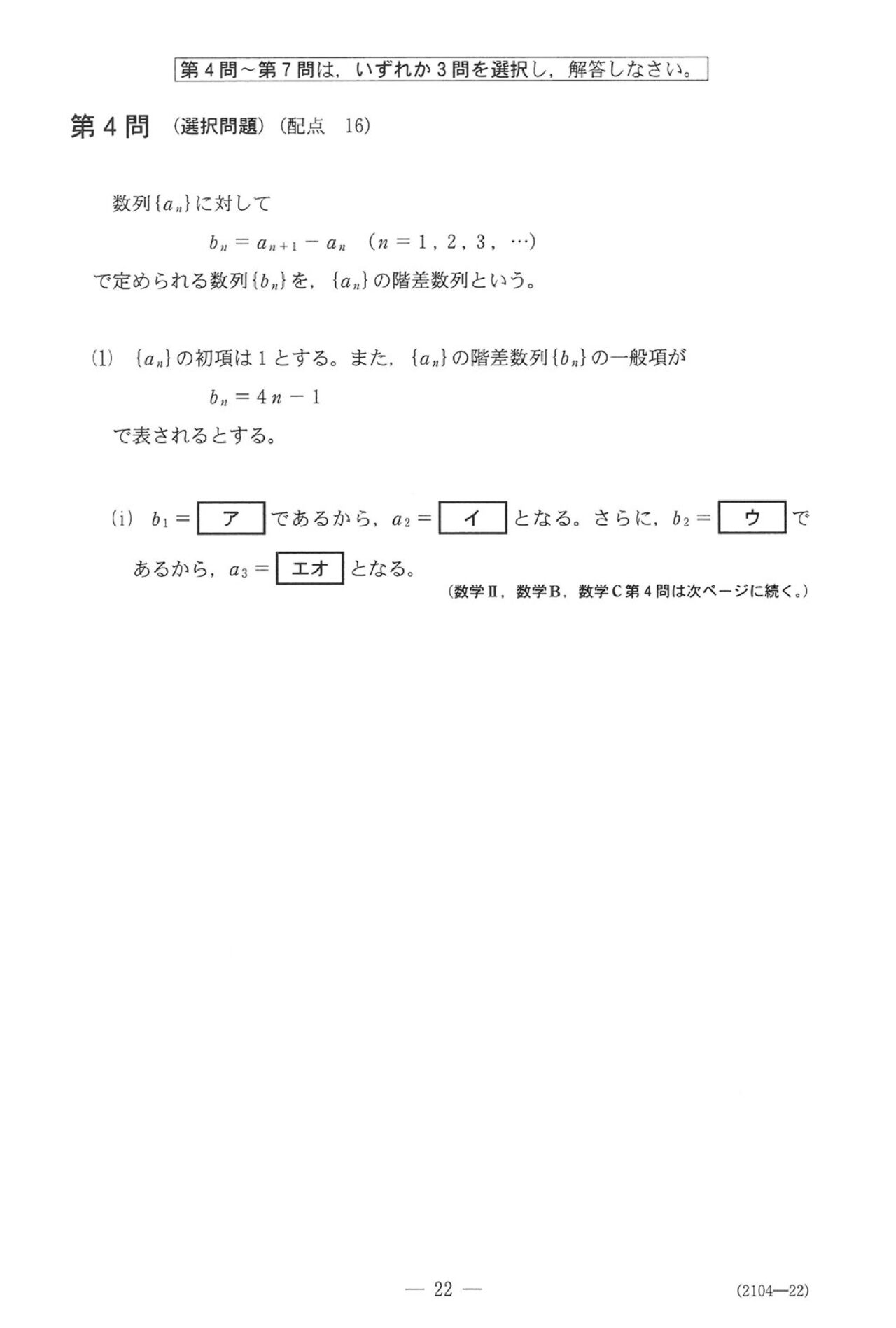
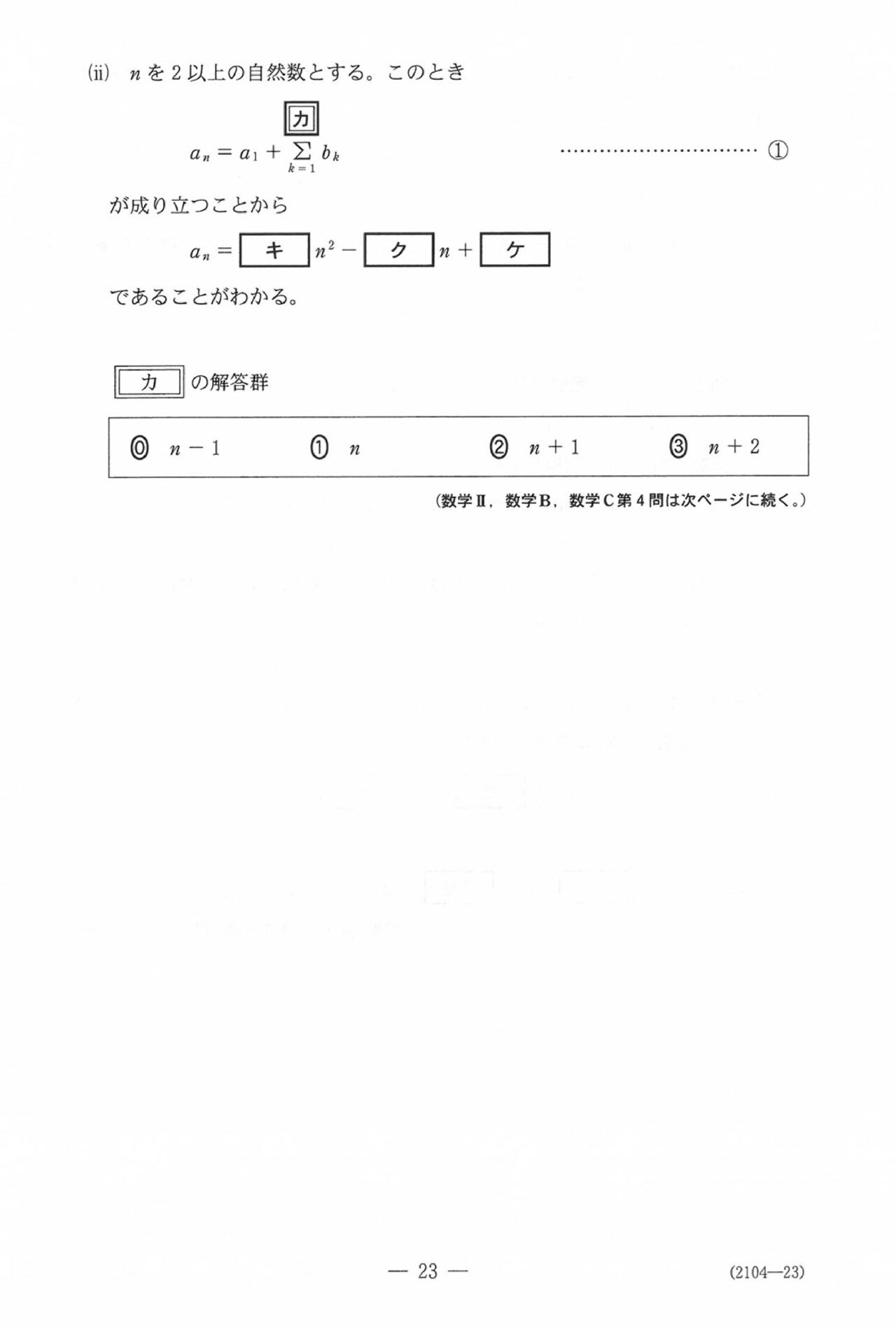
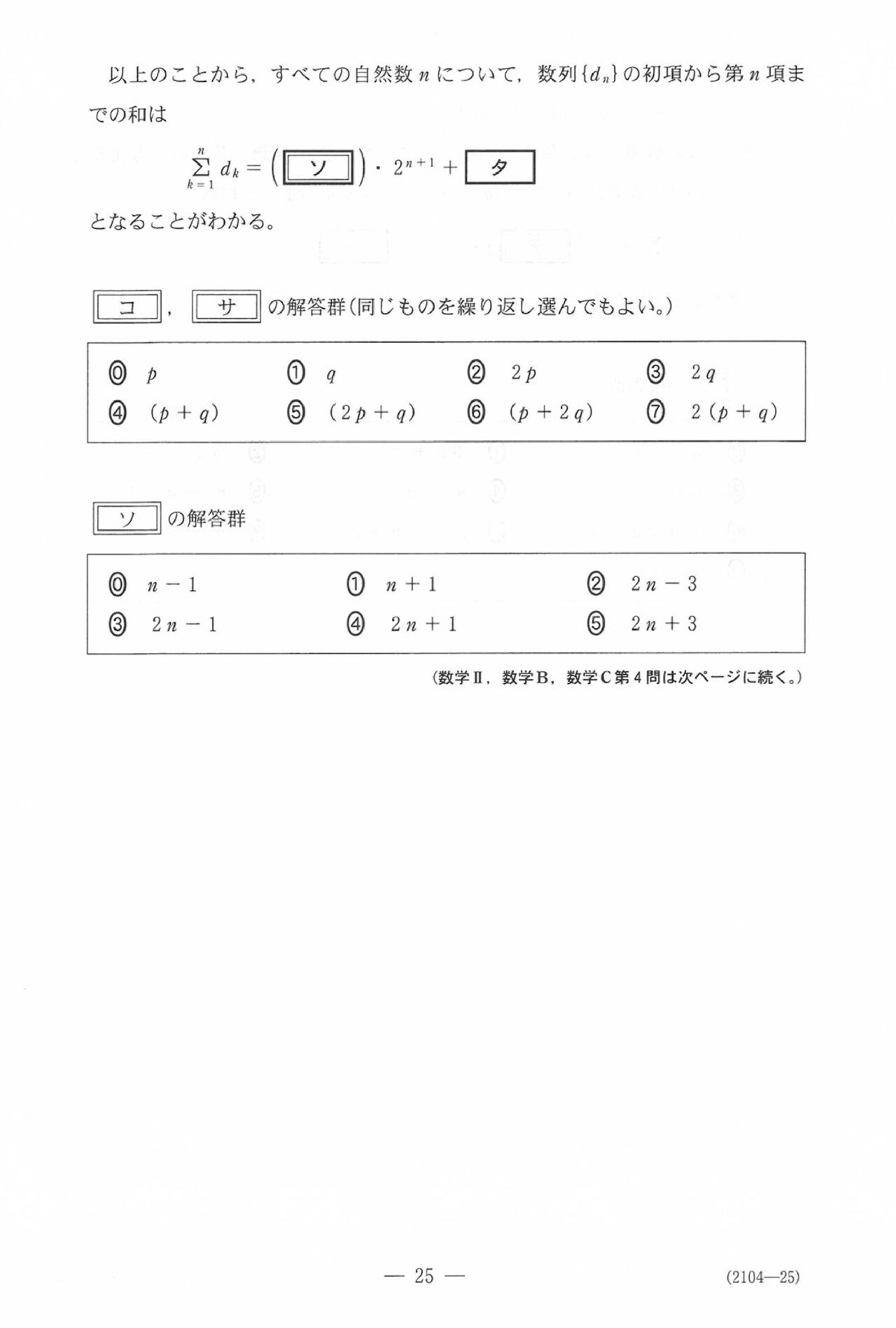
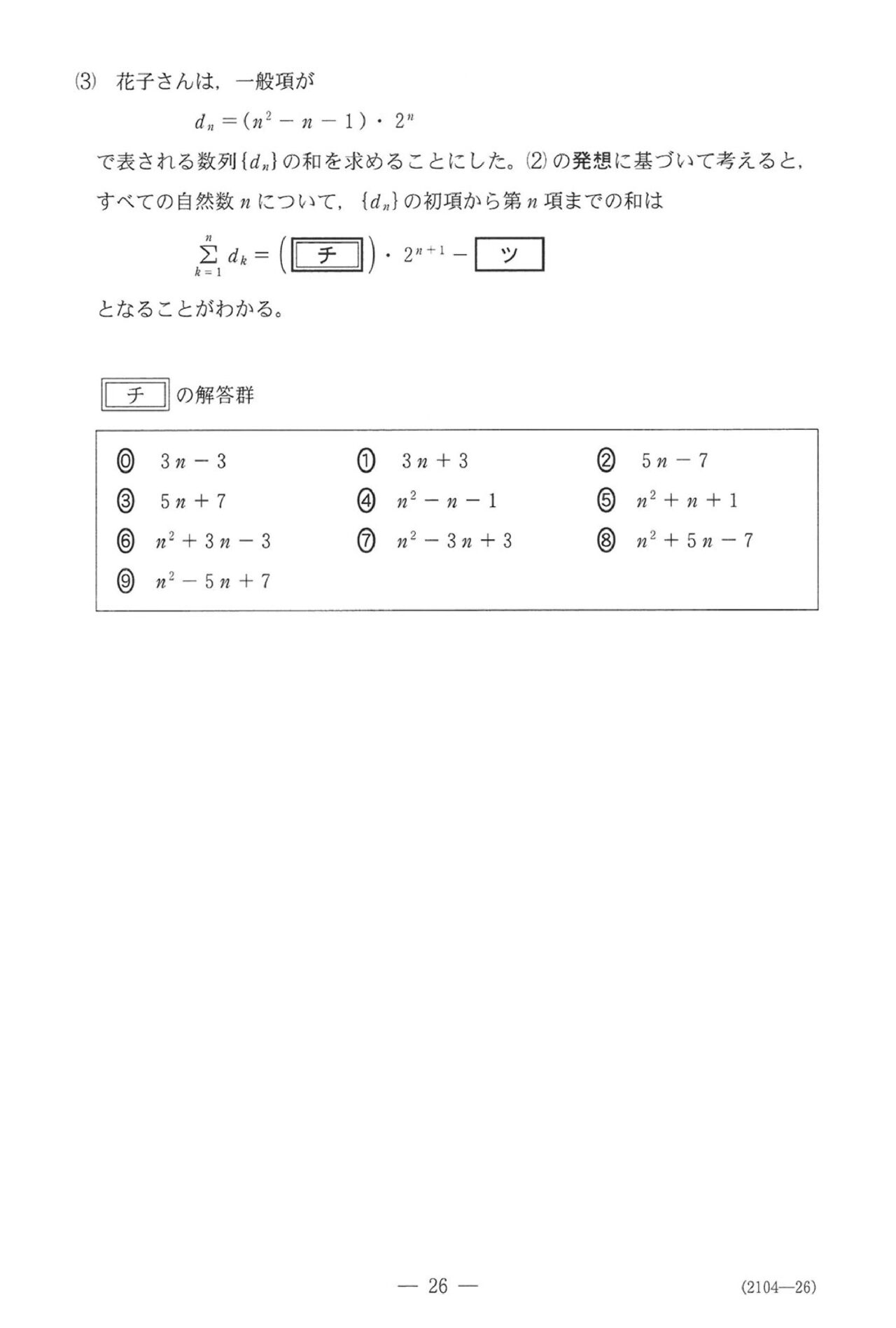
第４問

ここからは選択問題なんで、構成はいつもと一緒。第４問は数列です。

階差数列だからすぐに公式使いたいところなのに…

\(b_1\) とか \(a_2\) とか \(b_2\) とか \(a_3\) とか問われててマジうざいですね…

イライラせずに計算してください。

(3)の \(c_n\) の目標式設定ができなかった人は意外と多そうに感じます。めぐろ塾↓

君がそ～ゆ～授業を受けていることを祈りますm(_ _)m

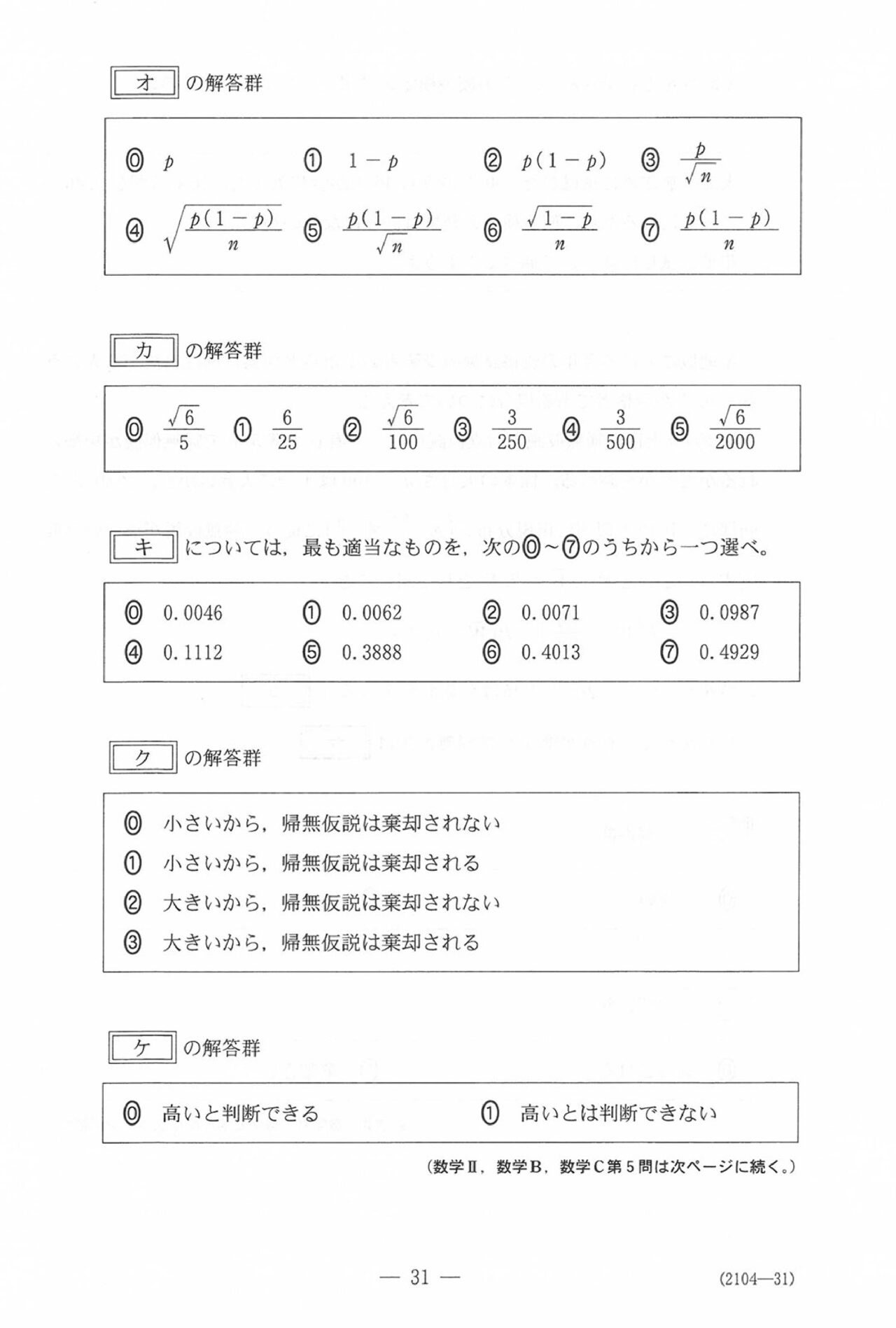
第５問

いつも通り、確率分布と統計的な推測。文系生徒はこれを解くしかないんですが…

去年以上に、解答枠周辺だけ読んでれば解ける出題なんで解きやすかったでしょう。

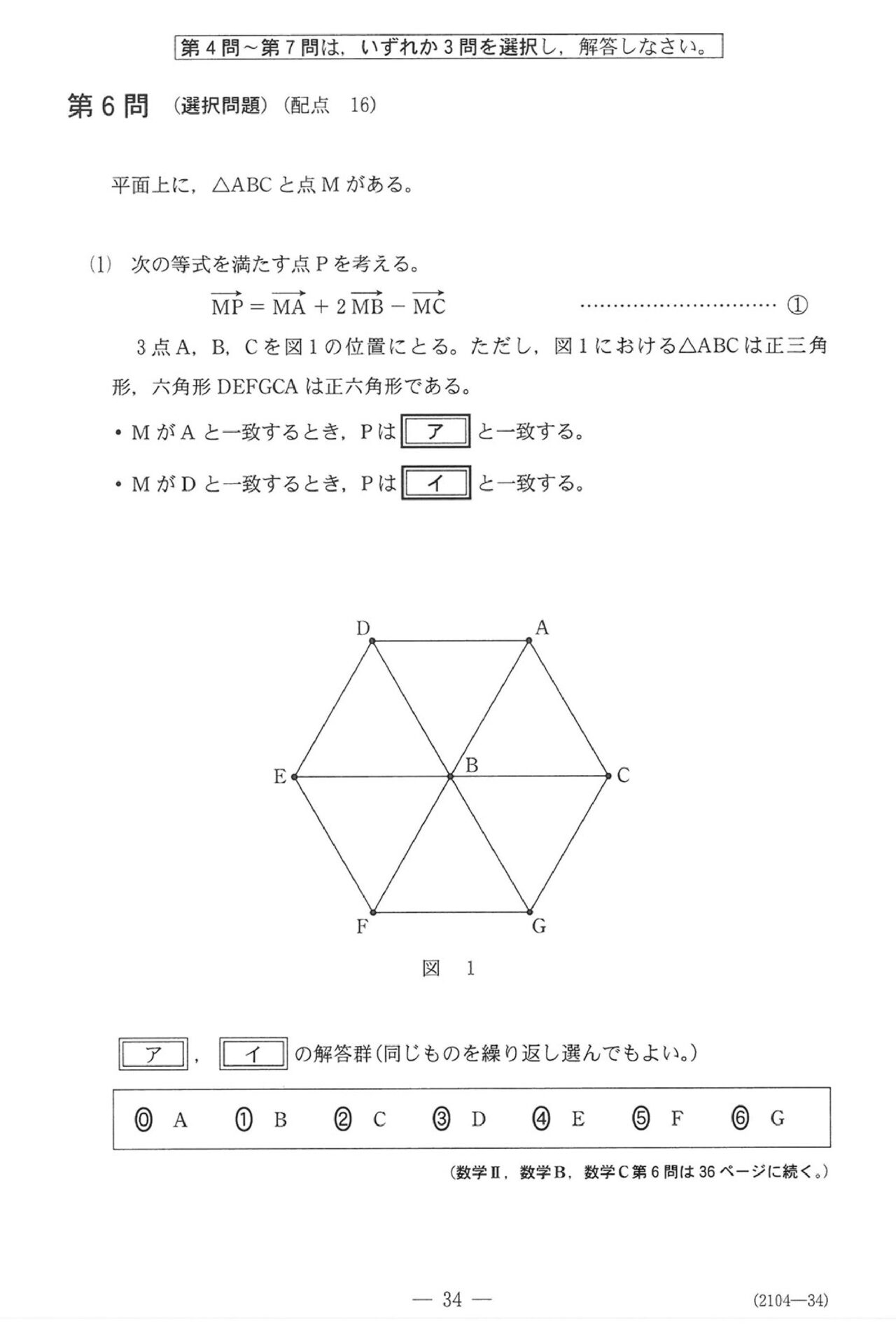
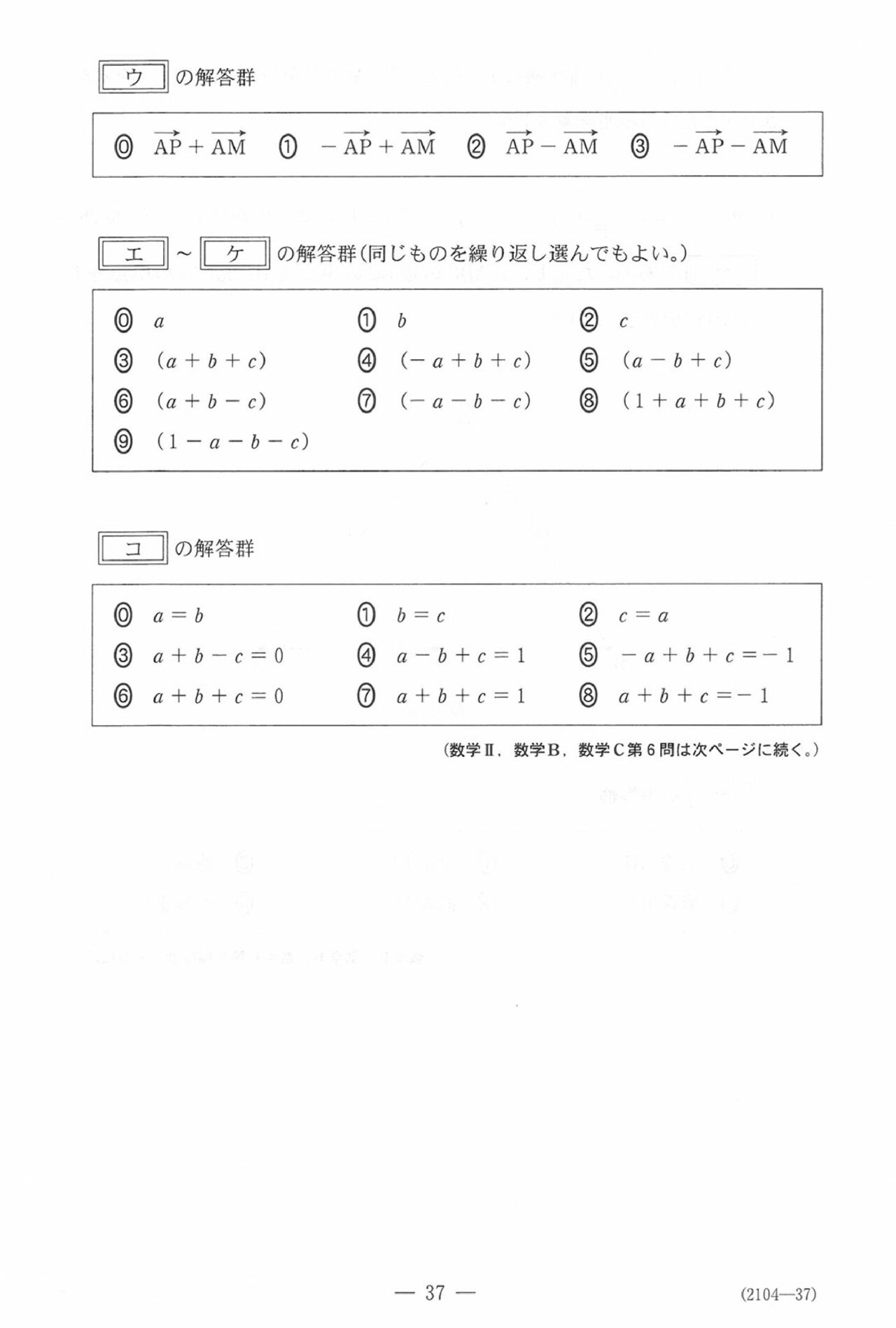
第６問

いつも通り、ベクトル。平面題材で、最後まで非常に穏やかです。計算もほぼほぼないってレベルです。

苦手にしてる受験生多いですよね…

ただ、めぐろ塾のテキストの一番最初に入れてるようなカンタン問題なので、何とか最後まで完答してもらいたい！

第７問

去年と同じく複素数平面、かつ最後に２次曲線も少し絡む内容でした。2025で上位校でメッチャ出題された、

って処理なんですが、問題文で極形式を導入してくれてるんで、経験がなくてもなんとかなる問題ではあります。

(3)は、

• (2)の結果を利用させる
• 複素数平面での平行移動
• 虚軸との位置関係で相加相乗平均の意識がいる

って良問。

全体的に計算量が少なく、類問の経験があったかどうかが大事な問題だったように思えます。

総評

ⅠＡは少し難化に感じましたが、ⅡＢは去年通り…

ってか正直式を選択肢形式で穴埋めるところが多すぎて、解答形式にめちゃくちゃイライラしました。この流れが今後も続くんだと…イヤですね…

あと、必答問題の構成が変わって、指数対数関数が出題されなかったのも気になるところです。来年は三角関数が出題されず、指数対数関数が出題されるって形になるかもしれません。昔はどっちかしか出ないって構成も多かったので。

因みに、カンタンカンタンって言ってきたプロ講師＝めぐろ塾の安田＝私めの出来は…

• 第１問の最後の領域をテキト―に選択してミス…　－2点
• 第３問の等積条件での通分ミス　－2点

で96点…

って言い訳するような恥ずかしい大人に皆さんがならないよう、めぐろ塾よりお祈り申し上げます(笑)

そして…

もう共テのことは忘れて私大に向けて勉強だっ！！

なお、本年も速報性を重視した記事にさせて頂きました。この記事を見ている高２生とかで、共テの詳しいテクニックとかを知りたい人は2023のⅠＡの記事↓をご参照ください。第１問→第２問→第５問→第３問の順で解けば、現行課程の対策にもなります。

また、今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！

君の大学受験が最高の結果になることを祈ってます！