2024慶應商【数学】解答速報

2024年2月14日2024年5月3日

2024慶應義塾大学商学部の数学の解答速報をお届けします！

めぐろ塾の安田

一個当てカンですいませんm(_ _)m

解答出してきた大手さんと答は一致してるんで許してください(笑)

Ⅰ

問題

考え方

めぐろ塾の安田

小問集合です。

(ⅰ)はただの指数計算、(ⅱ)は、

「積分区間が定数」の積分方程式
↓
定積分を未知数でおくと、関数 \(f(x)\) が２次式であることが分かる
↓
それを用いて、おきかえの式を定積分計算

とゆ～典型内容です。本年のセットでこの２つは絶対に落とせません。

めぐろ塾の安田

なのに僕は(ⅰ)の後半と(ⅱ)で見間違いによる計算ミスをしており、めぐろ塾の生徒に指摘されましたorzも～歳ですかね(笑)

(ⅲ)も、文字間に大小関係が設定されている３文字逆数和の不定方程式の整数解を求める問題なので、

最小値 \(a\) で逆数和を評価して\(a\) の範囲を絞り込み、\(a\) の可能性を確定
↓
２文字逆数和になるので、\(●bc+▲b+■c=0\) を因数分解し、素因数の拾い上げ

という整数での典型問題ですが、小問の内容としては重め。

(ⅳ)は個人的にトラウマレベルの問題です(笑)去年の解答速報↓

解答

Ⅱ

問題

考え方

めぐろ塾の安田

なんと、またしても小問集合です…

(ⅰ)は、小数第３位が５であることはすぐに分かるでしょう。小数第４位は、

\((3.606-0.000a)^2\)\(\:=3.606^2+2\cdot3.606\cdot+(0.000a)^2\)

より、\((0.000a)^2\) は小さすぎるので無視して、

\((3.606-0.000a)^2\)\(\:≒13.003236-2\cdot3.606\cdot0.000a\)

から、\(0.00326≒2\cdot3.606\cdot0.000a\) となる数字 \(a\) を探して考えますが…

めぐろ塾の安田

確証を得るための計算は面倒です。試験時間足りないんで、「\(a=4\) のときにかなり近いから小数第４位は５」ってしちゃった方がコスパはいいかも。

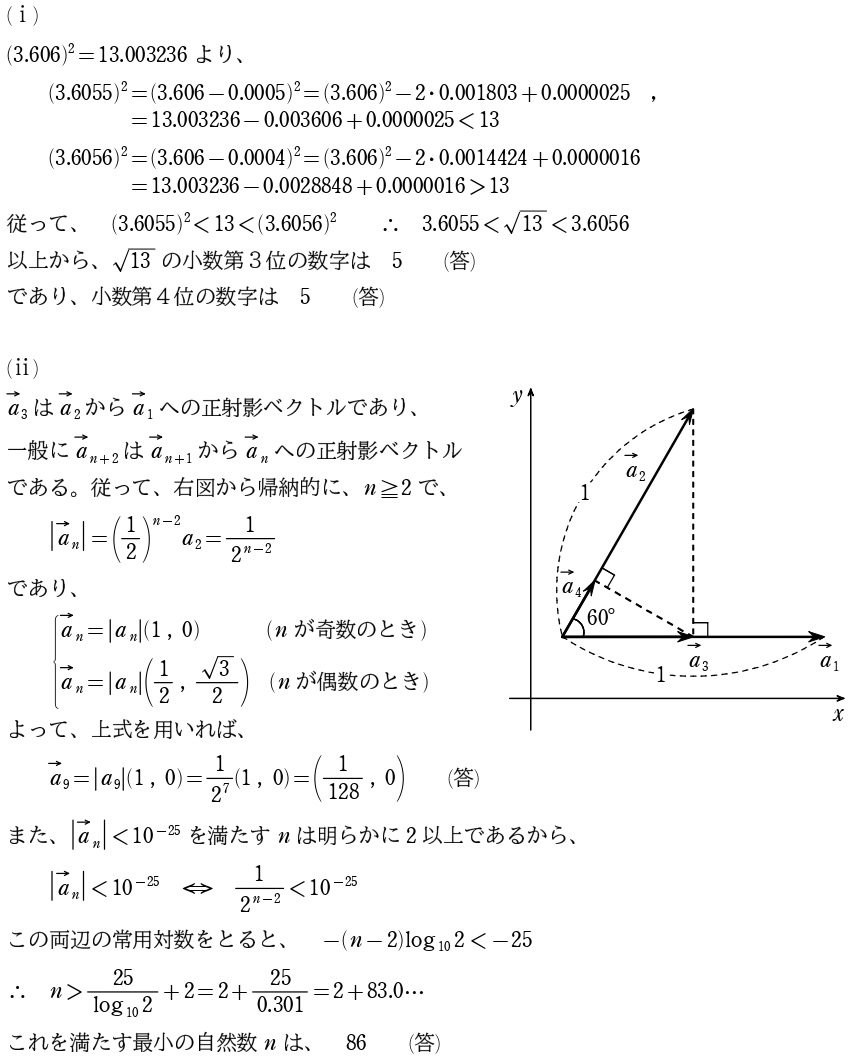
(ⅱ)は、「正射影ベクトル」↓を知っているかが全てです。

↑のように授業で扱っているめぐろ塾↓的中！

日本全国どこからでも受講可能！
完全個別指導コースあり（オンラインも可）！
初回面談・初回授業は完全個別で無料（オンラインも可）！

めぐろ塾の安田

初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓

お問い合わせ

03-6841-7626

電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。

頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。

X（Twitter）のDMからのお問い合わせ

受けた生徒が解けてて一安心しました。彼に問題送ってもらったんですが、「正射影ベクトル」って問題用紙に書いてて、僕へのアピールのように感じましたね(笑) \(a_{n+2}\) が \(a_{n+1}\) から \(a_n\) への正射影ベクトルであることさえ読み取れれば、図形的に偶数・奇数の場合が同じ方向になることが分かります。長さは有名直角三角形の比から１／２倍されていくので、後半の絶対値条件の不等式も常用対数をとって終わり。

(ⅲ)の前半は、\(a_1\) ～ \(a_6\) までを具体的に求めてみれば、\(n=5\) であることが分かります。後半はこの実験から、

\(a_2=2a_1\)　、　\(a_4=2a_3\)　に注目
↓
\(a_{2^k}\) はその前の項の２倍なんじゃね？

って気づけるかが全てです。解答の \(a_{n+1}=2a_n\) の証明は記述式としては甘いですが、マーク式なので簡易論証とさせて頂きます、悪しからずご了承くださいm(_ _)m

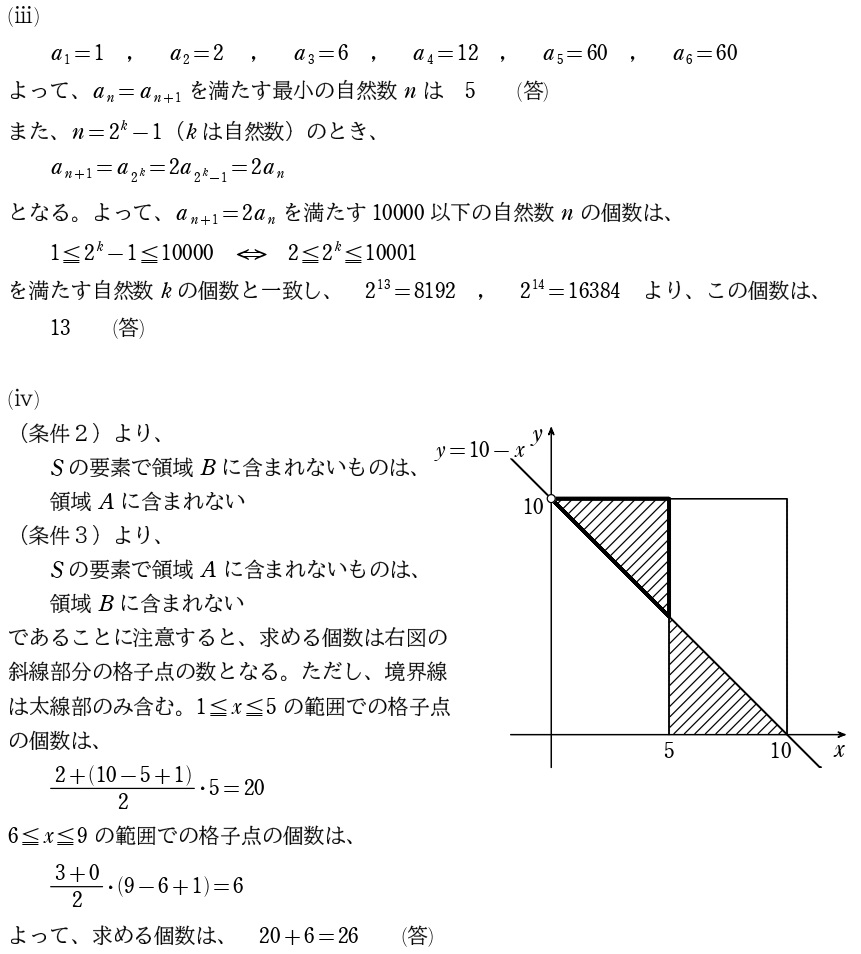
(ⅳ)はムズいです…\(A\) かつ \(B\) の領域の格子点の個数をカウントして「20個」としてしまった人が多いでしょう。でも…

めぐろ塾の安田

問題の書き方的に何かひっかけありそう…

って10分ほど熟考してみたところ…

（条件２）と（条件３）の対偶をとってみる
↓
\(\overline{A}\) かつ \(\overline{B}\) の領域もカウント対象

であることに気づきました。しかもこれに気づいても、こっちは境界線が含まれないから数えにくいってゆ～鬼畜仕様(笑)これは解けなくて良いでしょう。僕も「70分で解け」と言われたら捨てていると思います。

解答

Ⅲ

問題

考え方

めぐろ塾の安田

やっと大問です。しかも典型問題で有り難い。

(ⅰ)は連立した方程式を解くだけ。(ⅱ)はその結果を利用して面積計算です。インテグラルの区間が０～になるので、面積公式等のテクニックは使えません。

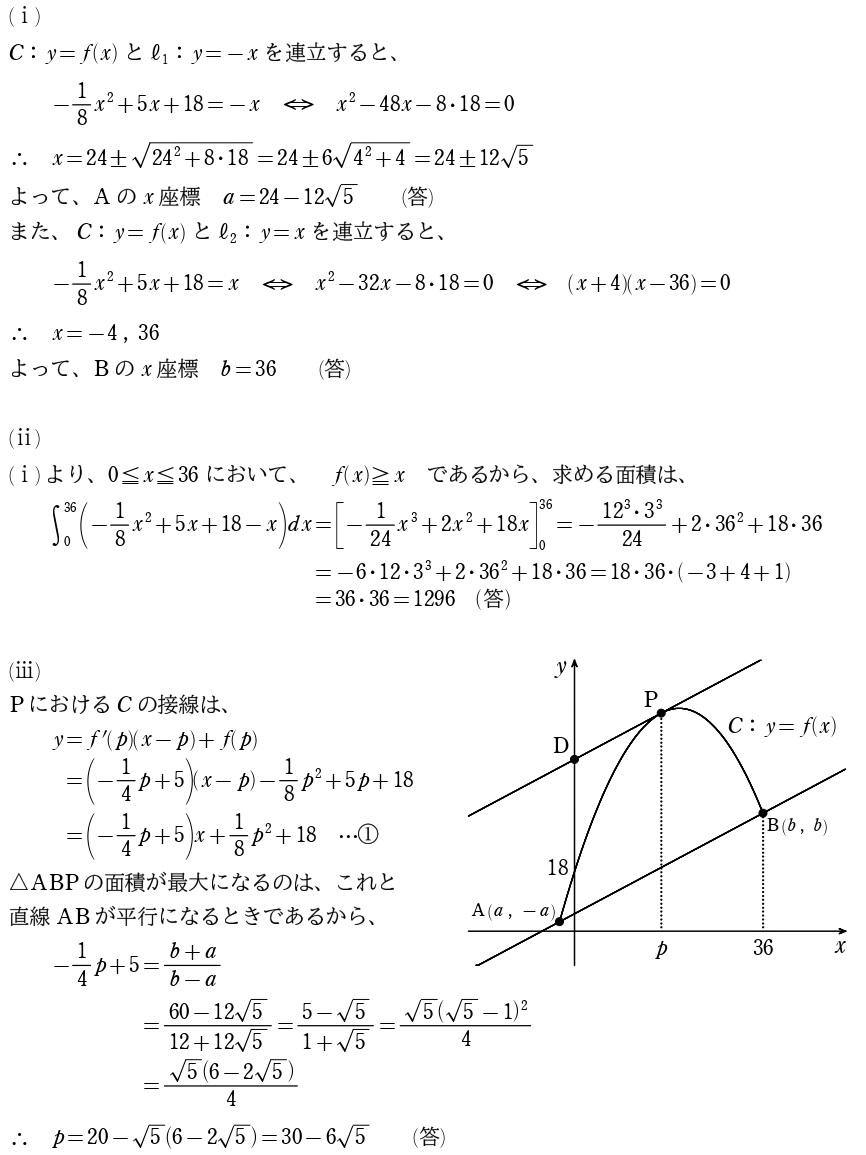
(ⅲ)は、

△ＡＢＰの面積の最大
↓
ＡＢを底辺として、高さの最大を考える
↓
Ｐは放物線上なので、ＡＢに平行な接線が引ける（その接点がＰとなる）とき

とゆ～、めぐろ塾の問題集に入れてるくらいの有名処理。(ⅳ)はただ接線の \(y\) 切片を計算するだけ。(ⅴ)も三角形の面積の最大ですが、

(ⅲ)のような図形的処理はムリ
↓
△ＢＤＰの面積 \(S\) を \(p\) の関数で立式

するしかありません。

三角形の面積公式（座標平面）

\((0\:,\:0)\:,\:(a\:,\:b)\:,\:(c\:,\:d)\) を頂点とする三角形の面積 \(S\) は、

\(S=\displaystyle\frac{1}{2}|ad-bc|\)

を使うと、絶対値の中が \(p\) の３次関数 \(g(p)\) となるので、微分して計算です。マーク式なので、絶対値の考慮や、解答のような増減表の作成はいらないでしょう。

極値のとこに決まってる！

って考えて、\(g'(p)=0\) の解のうち、\(0<p<36\) を満たすものを答としちゃいましょう。

めぐろ塾の安田

全体的に典型内容ではありますが、計算量は多めです。特に(ⅴ)のボリュームが多いので、(ⅳ)まで完答できれば大丈夫だと思います。

解答

Ⅳ

問題

考え方

(ⅰ)が、

場合分けして、総和の確率で１つを割ることで条件付き確率を求めましょう！

とゆ～出題者側からの誘導となっており、(ⅱ)と(ⅲ)はそれにならって自分で場合分けして計算していくだけなんですが…

めぐろ塾の安田

(ⅲ)の計算がメンドくさい…

最終的な値も複雑です。(ⅱ)まで当たってれば及第点に思えます。

解答

講評

めぐろ塾の安田

去年2023に比べて…

解答方式	試験時間	大問数	難易度
マーク式、一部答のみ解答	70分	４問	難化

です。2021～2023まで続いていた平坦な構成が、大幅に難化しました。

歴史的に、慶應商の数学の出題形式には統一感がありません。大問数が３～５問だったり、商業的題材の長文問題が出題されたりされなかったりで。でも、

小問集合が２つあるのは、2020以降で初

です。そして、共に最後の問題の難易度がヤバい…

めぐろ塾の安田

過去問対策を十分にやった人を地獄に叩き落す今年2024の作問は…個人的にはいかがなものかと感じでしまいました…

2021～2023とは異なり、70分という試験時間内で常人が満点を望むのは絶対ムリな構成です。

下手に時間をかけず、捨てる問題をバッサリ諦める勇気を持てたかが勝負！

のテストになってしまったかと思います。

因みに合格しためぐろ塾の生徒の各設問の正誤は↓の通りです。「一部合っていた」は「△」と表記します。

Ⅰ	(ⅰ)	〇
	(ⅱ)	〇
	(ⅲ)	△
	(ⅳ)	×
Ⅱ	(ⅰ)	△
	(ⅱ)	△
	(ⅲ)	△
	(ⅳ)	〇（当てカンが正解）
Ⅲ	(ⅰ)	〇
	(ⅱ)	〇
	(ⅲ)	〇
	(ⅳ)	〇
	(ⅴ)	×
Ⅳ	(ⅰ)	△
	(ⅱ)	〇
	(ⅲ)	×