2023共通テスト数学ⅡＢ解説～点数とるの重視で～

数学ⅠＡの解説記事↓

を書いたので…

やはり、「厳密性とかはすっ飛ばして、点数をとる！」をテーマにお届けします！

第１問

ア：⓪　、　イ：②　（答）

\(\sin 2x-\sin x=2\sin x\cos x-\sin x\)\(\:=\sin x(2\cos x-1)\)　（ウ、エの答）

①\(\:\:\Leftrightarrow\:\:\sin x>0\) かつ \(\cos x>\displaystyle\frac{1}{2}\)　、　②\(\:\:\Leftrightarrow\:\:\sin x<0\) かつ \(\cos x<\displaystyle\frac{1}{2}\)

\(0<x<\displaystyle\frac{\pi}{3}\)　、　\(\pi<x<\displaystyle\frac{5}{3}\pi\)　（オ～キの答）

和積公式 \(\sin A-\sin B=2\cos\displaystyle\frac{A+B}{2}\sin\displaystyle\frac{A-B}{2}\) より、\(\sin 4x-\sin 3x=2\cos\displaystyle\frac{7}{2}x\sin\displaystyle\frac{x}{2}\)

④\(\:\:\Leftrightarrow\:\:\)\(\cos\displaystyle\frac{7}{2}x>0\) かつ \(\sin\displaystyle\frac{x}{2}>0\)　（ク、ケの答）

⑤\(\:\:\Leftrightarrow\:\:\)\(\cos\displaystyle\frac{7}{2}x<0\) かつ \(\sin\displaystyle\frac{x}{2}<0\)

\(0<\displaystyle\frac{7}{2}x<\displaystyle\frac{\pi}{2}\:,\:\displaystyle\frac{3}{2}\pi<\displaystyle\frac{7}{2}x<\displaystyle\frac{5}{2}\pi\)

∴　\(0<x<\displaystyle\frac{\pi}{7}\:,\:\displaystyle\frac{3}{7}\pi<x<\displaystyle\frac{5}{7}\pi\)　（コ～セの答）

\(\displaystyle\frac{\pi}{7}<x<\displaystyle\frac{3}{7}\pi\:,\:\displaystyle\frac{5}{7}\pi<x<\pi\)

\(0<2x<\displaystyle\frac{\pi}{3}\:,\:\pi<2x<\displaystyle\frac{5}{3}\pi\)\(\:\:\Leftrightarrow\:\:0<x<\displaystyle\frac{\pi}{6}\:,\:\displaystyle\frac{\pi}{2}<x<\displaystyle\frac{5}{6}\pi\)

\(\displaystyle\frac{\pi}{7}<x<\displaystyle\frac{\pi}{6}\:,\:\displaystyle\frac{5}{7}\pi<x<\displaystyle\frac{5}{6}\pi\)　（ソ～チの答）

最初は対数の定義から、\(a^x=b\)　（ツの答）

\(\log_5{25}=2\)　、　\(\log_9{27}=\displaystyle\frac{3}{2}\)　（テ～ナの答）

\(\log_2{3}=\displaystyle\frac{p}{q}\:\:\Leftrightarrow\:\:2^\frac{p}{q}=3\)
の両辺を \(q\) 乗して、\(2^p=3^q\)　（ニの答）

(ⅱ)のときっぽいので、⑤　（ヌの答）

第２問

(1)より、\(x=\displaystyle\frac{2}{3}k=\displaystyle\frac{2}{3}\cdot9=6\) のとき、\(V\) は最大値 \(\displaystyle\frac{5}{3}\pi\cdot\displaystyle\frac{4}{27}k^3=\displaystyle\frac{5}{3}\pi\cdot\displaystyle\frac{4}{27}\cdot9^3\)\(\:=5\cdot4\cdot9\pi=180\pi\) をとる　（シ～ソの答）

\(\displaystyle\int_{0}^{30}\left(\displaystyle\frac{1}{5}x+3\right)dx=\left[\displaystyle\frac{1}{10}x^2+3x\right]_{0}^{30}\)\(\:=90+90=180\)　（タ～ツの答）

\(\displaystyle\int\left(\displaystyle\frac{1}{100}x^2-\displaystyle\frac{1}{6}x+5\right)dx\)\(\:=\displaystyle\frac{1}{300}x^3-\displaystyle\frac{1}{12}x^2+5x+C\)　（テ～ネの答）

解答群で「〇日後」を求める問題って把握したら、\(f(x)\) が冒頭の積分計算の被積分関数と同じであることに気づき、\(S(t)\) が400で開花するのか～…ほんでグラフの横軸が「日後」になってる。

以上から、\(S(t)=\displaystyle\int_{0}^{t}\left(\displaystyle\frac{1}{5}x+3\right)dx=400\) を解けばいいんじゃね？

∴　\(\displaystyle\frac{1}{10}t^2+3t=400\)

\(t=40\) は \(\displaystyle\frac{1}{10}\cdot40^2+3\cdot40=400\) を満たさない、
\(t=50\) は \(\displaystyle\frac{1}{10}\cdot50^2+3\cdot50=400\) を満たす。

∴　50日後　（ノの答）

増加グラフが作る同じ幅の面積は、後ろの方が大きいから、\(\displaystyle\int_{30}^{40}f(x)dx<\displaystyle\int_{40}^{50}f(x)dx\)　（ハの答）

40日後までは、\(\displaystyle\int_{0}^{30}f(x)dx+\displaystyle\int_{30}^{40}f(x)dx=180+115<400\)
50日後までは、\(\displaystyle\int_{0}^{30}f(x)dx+\displaystyle\int_{30}^{40}f(x)dx+\displaystyle\int_{40}^{50}f(x)dx\)\(\:>180+115+115>400\)

よって、開花日時は２月に入ってから40日後より後、かつ50日後より前　（ヒの答）

第３問

数学Ｂ「確率分布」からの出題ですが、ほとんどの私大・国立２次が出題範囲から外しているため、勉強していない受験生が多いでしょう。

2025共通テスト受験者はほぼ必須になる内容なんで一応解説しますが…

ページ順変わっちゃうけど、取りあえず正規分布表から↓

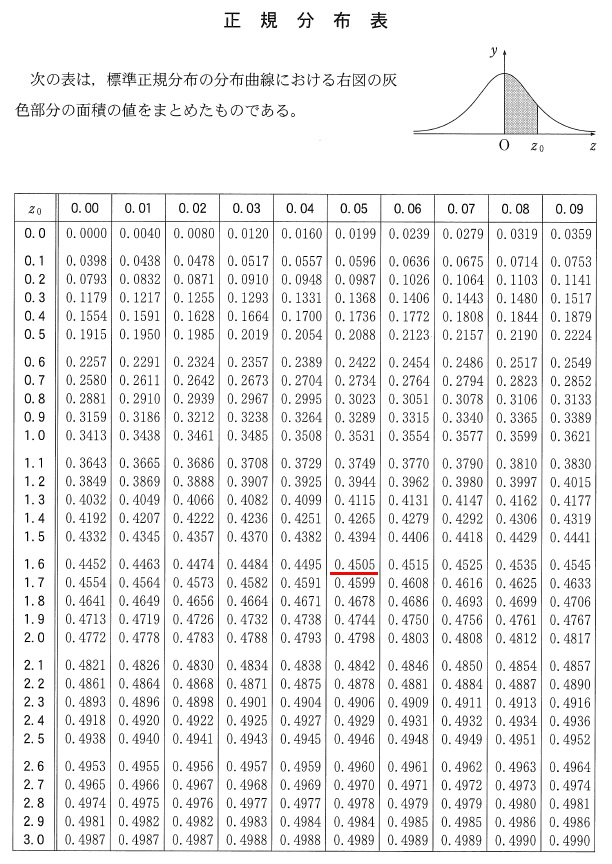
以下は問題ページを順に↓

\(\sigma>0\) より、\(X≧m\:\:\Leftrightarrow\:\:\displaystyle\frac{X-m}{\sigma}≧0\)　（アの答）

この確率は正規分布の半分なので、\(\displaystyle\frac{1}{2}\)　（イの答）

\(E(\overline{X})=m\)　、　\(\sigma(\overline{X})=\displaystyle\frac{\sigma}{\sqrt{n}}\)　（エ、オの答）

面積が0.901÷2＝0.4505となる \(z_0\) は正規分布表の赤部分で、1.65　（カ～クの答）

\(-1.65≦\displaystyle\frac{\overline{X}-m}{\displaystyle\frac{\sigma}{\sqrt{n}}}≦1.65\)　\(\Leftrightarrow\:\:-1.65≦\displaystyle\frac{30-m}{\displaystyle\frac{3.6}{\sqrt{400}}}≦1.65\)　\(\Leftrightarrow\:\:-1.65\times0.18≦30-m≦1.65\times0.18\)

\(1.65\times0.18≒1.5\times\displaystyle\frac{1}{5}≒0.3\) より、\(30-0.3≦m≦30+0.3\)
∴　\(29.7≦m≦30.3\)　（ケの答）

「Sサイズである確率」＝「母平均を下回る確率」ってだけ読み取れれば、冒頭でもやってる通りで、\(\displaystyle\frac{1}{2}\)　（コ、サの答）

次は、式が独立試行の定理の形であることに気づければ、50個から25個選ぶと考えて、\({}_{50}\textrm{C}_{25}\)　（シ、スの答）

二項分布 \(B\left(50+k\:,\:\displaystyle\frac{1}{2}\right)\) について、

平均は、\((50+k)\cdot\displaystyle\frac{1}{2}=\displaystyle\frac{50+k}{2}\)

分散は、\((50+k)\cdot\displaystyle\frac{1}{2}\cdot\left(1-\displaystyle\frac{1}{2}\right)=\displaystyle\frac{50+k}{4}\)

よって、正規分布 \(N\left(\displaystyle\frac{50+k}{2}\:,\:\displaystyle\frac{50+k}{4}\right)\) に従う　（セ、ソの答）

\(25≦U_k≦25+k\)　\(\Leftrightarrow\:\:{\small25-\displaystyle\frac{50+k}{2}≦U_k-\displaystyle\frac{50+k}{2}≦25+k-\displaystyle\frac{50+k}{2}}\)　\(\Leftrightarrow\:\:-\displaystyle\frac{k}{2}≦U_k-\displaystyle\frac{50+k}{2}≦\displaystyle\frac{k}{2}\)　\(\Leftrightarrow\:\:-\displaystyle\frac{\displaystyle\frac{k}{2}}{\sqrt{\displaystyle\frac{50+k}{4}}}≦\displaystyle\frac{U_k-\displaystyle\frac{50+k}{2}}{\sqrt{\displaystyle\frac{50+k}{4}}}≦\displaystyle\frac{\displaystyle\frac{k}{2}}{\sqrt{\displaystyle\frac{50+k}{4}}}\)

∴　\(-\displaystyle\frac{k}{\sqrt{50+k}}≦Y≦\displaystyle\frac{k}{\sqrt{50+k}}\)　（タの答）

\(k=\alpha\:,\:\sqrt{50+k}=\beta\) より、\(\alpha^2≧4\beta^2\)　\(\Leftrightarrow\:\:k^2≧4(50+k)\)　\(\Leftrightarrow\:\:(k-2)^2≧204\)

これを満たす最小の自然数 \(k=k_0\) は \(k-2=15\) のときで、\(k_0=17\)　（チ、ツの答）

第４問

\(a_3=1.01\{1.01(10+p)+p\}+p\)　（アの答）

\(a_{n+1}=1.01a_n+p\)　（イ、ウの答）

\(\alpha=1.01\alpha+p\)　\(\Leftrightarrow\:\:-0.01\alpha=p\)　\(\Leftrightarrow\:\:\alpha=-100p\)　より、
\(a_{n+1}+100p=1.01(a_n+100p)\)　（エ、オの答）

「もともと預金口座にあった10万円」と同様に、１年目の初めに入金した \(p\) 万円は、ｎ年目の初めには \(p\times1.01^{n-1}\) 万円になる　（カの答）

２年目の初めに入金した \(p\) 万円は、ｎ年目の初めには \(p\times1.01^{n-2}\) 万円になる　（キの答）

\(a_n=10\times1.01\:+\)\(\:p+p\times1.01+p\times1.01^2\)\(\:+\:\cdots\cdots\)\(\:+\:p\times1.01^{n-2}+p\times1.01^{n-1}\)
\(\:=10\times1.01\:+\)\(\:p\displaystyle\sum_{k=1}^{n}1.01^{k-1}\)　（クの答）

\(\displaystyle\sum_{k=1}^{n}1.01^{k-1}=\displaystyle\frac{1.01^n-1}{1.01-1}\)\(\:=100(1.01^n-1)\)　（ケの答）

\(1.01a_{10}≧30\)　（コの答）

\(a_{n+1}+100p=1.01(a_n+100p)\) より \(a_{10}+100p=(a_1+100p)\cdot1.01^9\) なので、上式は、\((a_1+100p)\cdot1.01^{10}-101p≧30\) であり、\(a_1=10+p\) を用いると、

\((101p+10)\cdot1.01^{10}-101p≧30\)　\(\Leftrightarrow\:\:101p(1.01^{10}-1)≧30-10\cdot1.01^{10}\)
∴　\(p≧\displaystyle\frac{30-10\times1.01^{10}}{101(1.01^{10}-1)}\)　（サ～セの答）

が分かるので、\(3\times1.01^{n-1}\) 万円多い　（ソの答）

第５問

ＢＣの中点がＭなので、\(\overrightarrow{\textrm{AM}}=\displaystyle\frac{1}{2}\overrightarrow{\textrm{AB}}+\displaystyle\frac{1}{2}\overrightarrow{\textrm{AB}}\)　（ア～エの答）

内積の定義式から、\(\displaystyle\frac{\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AB}}}{\left|\overrightarrow{\textrm{AP}}\right|\left|\overrightarrow{\textrm{AB}}\right|}=\cos\angle\textrm{PAB}\)\(\:=\cos\theta\)　（オの答）

\(\left|\overrightarrow{\textrm{PB}}\right|=3\) の両辺を２乗して、\(\left|\overrightarrow{\textrm{AB}}-\overrightarrow{\textrm{AP}}\right|^2=9\)　\(\Leftrightarrow\:\:3^2-2\overrightarrow{\textrm{AB}}\cdot\overrightarrow{\textrm{AP}}+\left(3\sqrt{2}\right)^2=9\)　\(\Leftrightarrow\:\:\overrightarrow{\textrm{AB}}\cdot\overrightarrow{\textrm{AP}}=9\)　（カの答）

\(\overrightarrow{\textrm{AD}}=t\overrightarrow{\textrm{AM}}\) とおくと、\(\angle\textrm{APD}=90^\circ\) より、\(\overrightarrow{\textrm{PA}}\cdot\overrightarrow{\textrm{PD}}=0\)　\(\Leftrightarrow\:\:\overrightarrow{\textrm{AP}}\cdot\left(\overrightarrow{\textrm{AP}}-\overrightarrow{\textrm{AD}}\right)=0\)　\(\Leftrightarrow\:\:\left|\overrightarrow{\textrm{AP}}\right|^2-t\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AM}}=0\)　\(\Leftrightarrow\:\:18-t\displaystyle\frac{\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AC}}}{2}=0\)　\(\Leftrightarrow\:\:18-t\displaystyle\frac{9+9}{2}=0\)　　∴　\(t=2\)　（キの答）

\(\overrightarrow{\textrm{AQ}}=\overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{AC}}\) であり、\(\overrightarrow{\textrm{PA}}\cdot\overrightarrow{\textrm{PQ}}=0\)　\(\Leftrightarrow\:\:\overrightarrow{\textrm{AP}}\cdot\left(\overrightarrow{\textrm{AP}}-\overrightarrow{\textrm{AQ}}\right)=0\)　\(\Leftrightarrow\:\:\left|\overrightarrow{\textrm{AP}}\right|^2=\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AQ}}\)
∴　\(\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AB}}+\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AC}}=\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AP}}\)　（クの答）

①より、\(\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AB}}=\left|\overrightarrow{\textrm{AP}}\right|\left|\overrightarrow{\textrm{AB}}\right|\cos\theta\) 、\(\overrightarrow{\textrm{AP}}\cdot\overrightarrow{\textrm{AC}}=\left|\overrightarrow{\textrm{AP}}\right|\left|\overrightarrow{\textrm{AC}}\right|\cos\theta\) を上式に代入し、\(\left|\overrightarrow{\textrm{AP}}\right|\) で両辺を割ると、
\(\left|\overrightarrow{\textrm{AB}}\right|\cos\theta+\left|\overrightarrow{\textrm{AC}}\right|\cos\theta=\left|\overrightarrow{\textrm{AP}}\right|\)　（ケの答）

ここと同様にして、\(k\left|\overrightarrow{\textrm{AP}}\right|\left|\overrightarrow{\textrm{AB}}\right|\cos\theta=\left|\overrightarrow{\textrm{AP}}\right|\left|\overrightarrow{\textrm{AC}}\right|\cos\theta\)
∴　\(k\left|\overrightarrow{\textrm{AB}}\right|=\left|\overrightarrow{\textrm{AC}}\right|\)　（コの答）

\(\left|\overrightarrow{\textrm{AB}}\right|\cos\theta\)\(\:+\:k\left|\overrightarrow{\textrm{AB}}\right|\cos\theta=\left|\overrightarrow{\textrm{AP}}\right|\)

直角三角形ＡＢＢ′ に注目すると、\(\left|\overrightarrow{\textrm{AB}}\right|\cos\theta=\left|\overrightarrow{\textrm{AB’}}\right|\)

上の式にこれを代入すると、\(\left|\overrightarrow{\textrm{AB’}}\right|+k\left|\overrightarrow{\textrm{AB’}}\right|=\left|\overrightarrow{\textrm{AP}}\right|\)　\(\Leftrightarrow\:\:\left|\overrightarrow{\textrm{AB’}}\right|=\displaystyle\frac{1}{k+1}\left|\overrightarrow{\textrm{AP}}\right|\)

よって、\(\textrm{B’}\) は線分 \(\textrm{AP}\) を \(1:k\) に内分する点

同様に直角三角形ＡＣＣ′ に注目すると、\(\left|\overrightarrow{\textrm{AC}}\right|\cos\theta=\left|\overrightarrow{\textrm{AC’}}\right|\)
であり、(ⅰ)の最終式から \(\left|\overrightarrow{\textrm{AB}}\right|\) を消去すると、\(\displaystyle\frac{\left|\overrightarrow{\textrm{AC}}\right|}{k}\cos\theta+\left|\overrightarrow{\textrm{AC}}\right|\cos\theta=\left|\overrightarrow{\textrm{AP}}\right|\) であるから、\(\left|\overrightarrow{\textrm{AC’}}\right|+k\left|\overrightarrow{\textrm{AC’}}\right|=k\left|\overrightarrow{\textrm{AP}}\right|\)　\(\Leftrightarrow\:\:\left|\overrightarrow{\textrm{AC’}}\right|=\displaystyle\frac{k}{k+1}\left|\overrightarrow{\textrm{AP}}\right|\)

よって、\(\textrm{C’}\) は線分 \(\textrm{AP}\) を \(k:1\) に内分する点で、④　（サの答）

二等辺に決まってて、①の「∠ＰＢＡ＝90°」とか意味不明だから、②　（シの答）

講評

第１問

前半の「三角関数」はそこそこ面倒くさかったですね。

ただ解説でも言った通り、「指数対数関数」からの出題は過去最大級に簡単でした。

第２問

前半の最大・最小はその前の３次関数の結果を流用できることからも、計算量が少なく簡単です。

後半の「ソメイヨシノ」は…

ってゆーセンター試験最後半からの傾向に対する対策を意識してない人はビックリしたかもしれませんが…

第３問

難しくも簡単でもなく、至っていつも通り。

「ピーマン分類法」とかわけのわからねー言葉で文章量を増やしているのは、センター試験最後半からの数学全体の傾向なので、やはり真面目に読まないようにしましょう(笑)

第４問

ⅡＢも難しかった2022共通テストの「数列」は、やはり文章が不要に長かったですが…

「複利計算」ってゆー珍しいネタであることを考慮しても、いつもより簡単です。

因みに、「方針１」と「方針２」を穴埋めさせ、最後は好きな方でどうぞ～、ってゆー構成は、共通テストのプレテストの「数列」でも出題（漸化式の解法）されていました。

今後の共通テストでもこういった構成で出題される可能性は高いので…

こーゆーのできてない人は、

とか、

って割り切りを持って解いた方がいいです。

第５問

最後はそこそこ難しかったと思いますが…

ので、いつも通りって感じです。

センター試験最後半から、ベクトルの最後は計算ではなく、「文章の選択肢から、状況を解答させる」ことが多いです。

解説でも軽く言いましたが…

総評

解き終わって、特に印象に残った問題がありませんでした。

計算量的に言っても、「過去のセンター試験ⅡＢまで遡っても、かなり簡単な年」って感じです。

• 第５問の内積計算で、値を見間違える　－２点

で98点…

まとめ

「解答速報」ってカテゴリーで記事にしてるんですが…「解答速報」って名乗れるスピードでの投稿じゃなくなっちゃいました(笑)

今年のインフルエンザはヤバいので、特に受験生は絶対にかからないように！！

君の大学受験が最高の結果になることを祈ってます！