上智大学の数学を徹底解説!

 めぐろ塾の安田
めぐろ塾の安田早稲田理工卒、上智理工補欠不合格(笑)
数学の講師歴20年を超える私めが…
上智大学の数学を徹底解説します!
上智大学の位置づけ
「一番偏差値が信頼できるのは河合塾の全統記述模試である」ってことについては↓の記事をご参照くださいm(_ _)m


河合塾の2025入試難易予想ランキング表(私立大)を上の方だけ掲載します。



文系からは「経済・経営・商学系」を↓
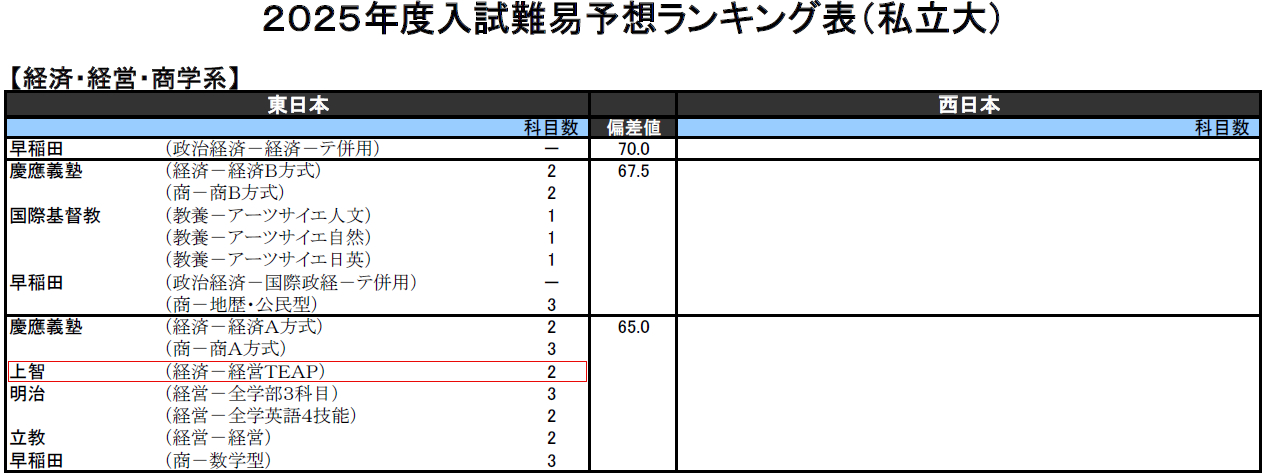




理系からは「理学系」を↓
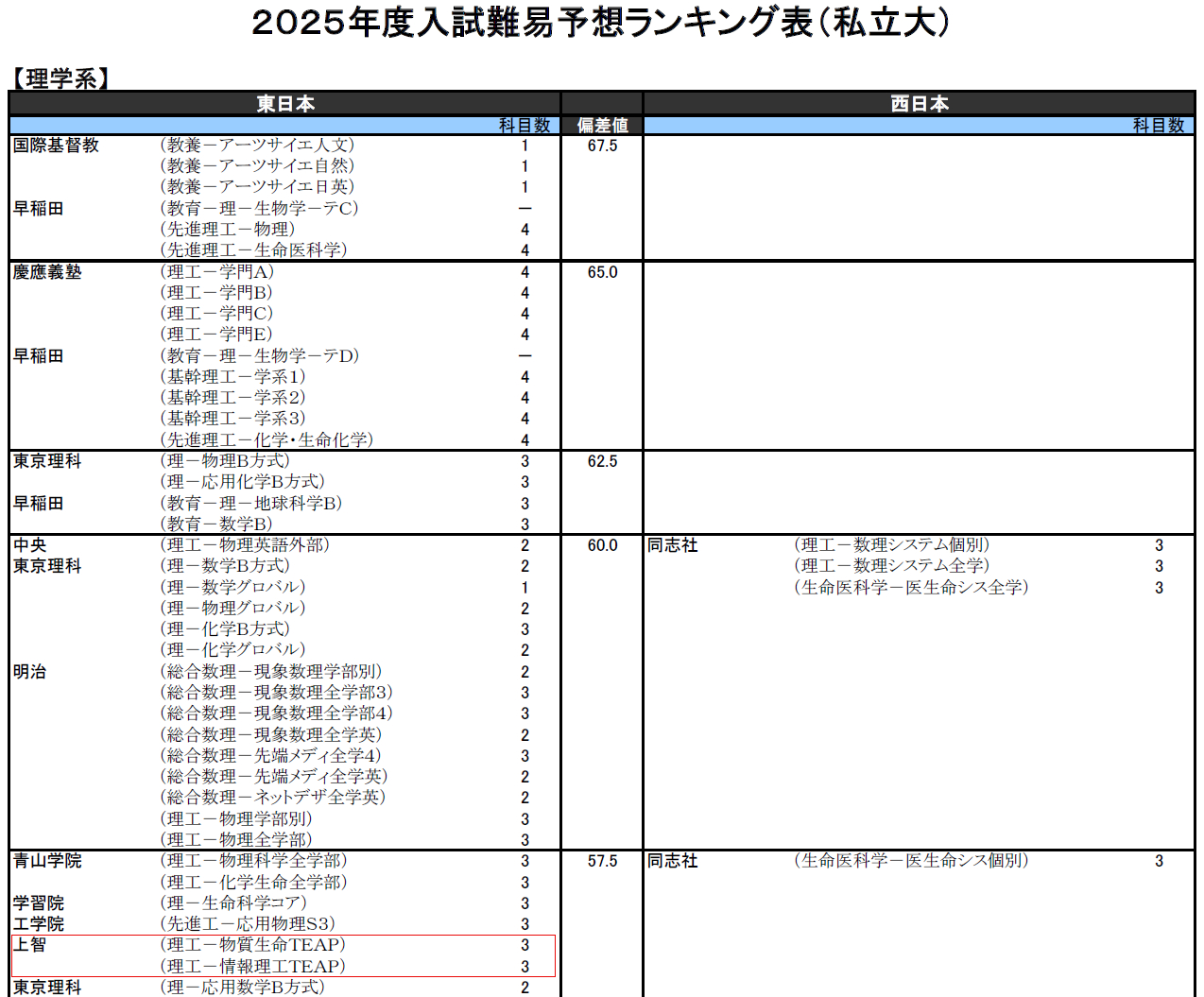

どちらも上位に顔を出します。
「早慶上理」=「早稲田・慶應・上智・理科大」
という古くからのくくりがある通り、
「GMARCH」=「学習院・明治・青学・立教・中央・法政」
と早慶の中間、というのが、上智大学の位置づけです。



理系で言うと「≒理科大」とされています。最近では、
「SMART」=「上智・明治・青学・立教・理科大」
なんてくくりも使われており、首都圏上位大学として君臨しています。
上智大学の入試の種類と数学
上智大学の入試の種類
2021の大学入学共通テスト開始に合わせて、以下の3種類に大分されています。
| ①TEAPスコア利用方式 | 他学で言う「全学統一日程入試」に当たる方式。 以下本記事では「TEAP利用」と呼称。 |
|---|---|
| ②学部学科試験・共通テスト併用方式 | 他学で言う「学部別・一般入試」に当たる方式。 以下本記事では「共テ併用」と呼称。 |
| ③共通テスト利用方式 | 共通テストの点数のみで決まる方式。 本記事では対象としません。 |
上智大学独自試験の数学の種類
前項に伴い、上智大学独自試験の数学は、文系2種類・理系2種類となっています。
解いてね~ヤツに偉そ~に解説されたくね~



って思われるのもイヤなんで、2023以降については全部「解説・解答・講評」や「解答速報」を作成しています↓併せてご参照くださいm(_ _)m
文系TEAP利用
経済共テ併用
理工TEAP利用
理工共テ併用
経済学部以外を志望する文系の人
数学を使って受験できるのは「TEAP利用」のみです。「共テ併用」では使えません、数学得意な人は残念(笑)
経済学部志望の人
「TEAP利用」・「共テ併用」共に、数学で受験可能です。
因みに「TEAP利用」では理系受験も可能で、この場合「理工TEAP利用」の数学を解くことになります。
理系の人
当然ではありますが、「TEAP利用」・「共テ併用」共に、数学は必須です。
| ①TEAPスコア利用方式 | 理科が2科目必要 |
|---|---|
| ②学部学科試験・共通テスト併用方式 | 理科が1科目で済む |
「TEAP利用」では早慶理工と同様に理科が2科目必要ですが、「共テ併用」では理科大以下と同様に理科が1科目で済みます。



僕みたいに、
「物理は得意!でも化学は苦手…」
って人に「共テ併用」はオススメです!
文理共通のアドバイス
2021~2025の出題と解答方式
2021~2025の出題と解答方式を表にまとめると↓のようになります。因みにここでは、「答のみ解答(途中過程が問われない)」もマーク式として扱います。
| 種類 | 年度 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 文系TEAP利用 | 2025 | 2次と円の共有点・面積 マーク式 | 空間座標 マーク式 | 小問集合 マーク式 | 条件付き確率 マーク式 |
| 2024 | 空間図形 マーク式 | 確率 マーク式 | 小問集合 マーク式 | ||
| 2023 | 三角関数の最大・最小 マーク式 | ベクトル(正八面体) マーク式 | 条件付き確率 マーク式 | 小問集合(集合・命題アリ) マーク式 | |
| 2022 | グラフと確率 マーク式 | ベクトル(立方体) マーク式 | 3次のグラフと面積 マーク式 | 小問集合(集合・命題アリ) マーク式 | |
| 2021 | 小問集合 マーク式 | 2次のグラフの接線と面積 マーク式 | 3次のグラフと確率 マーク式 | 小問集合(集合・命題アリ) マーク式 | |
| 経済共テ併用 | 2025 | 2変数関数の最大・最小 マーク式 | 平面ベクトル マーク式 | 小問集合(集合・命題アリ) マーク式 | |
| 2024 | 小問集合 マーク式 | 空間座標 マーク式 | 定積分関数 マーク式 | ||
| 2023 | 小問集合 マーク式 | 4次のグラフの極値と接線 マーク式 | 正五角形と黄金比 マーク式 | ||
| 2022 | 小問集合 マーク式 | 空間座標 (1)~(3)のうち、(3)のみ記述式 | 確率 マーク式 | ||
| 2021 | 小問集合(集合・命題アリ) マーク式 | 確率漸化式 マーク式 | 2次・3次のグラフと面積 (1)~(3)のうち、(2)のみ記述式 | ||
| 理工TEAP利用 | 2025 | 定積分の評価 記述式 | 確率 マーク式 | 水量問題(ほぼ非回転体の体積) マーク式 | ベクトル(四角錐) マーク式 |
| 2024 | 小問集合 マーク式 | ベクトル(四角錐) マーク式 | Ⅲのグラフと積分 記述式 | 3項間漸化式と証明 記述式 | |
| 2023 | 小問集合 マーク式 | ベクトル(立方体) マーク式 | 水量問題(ほぼ \(y\) 軸回転体の体積) マーク式 | Ⅲの不等式証明と帰納法 記述式 | |
| 2022 | 小問集合(集合・命題アリ) マーク式 | ベクトル(立方体) マーク式 | 確率 マーク式 | 極座標と媒介変数表示 記述式 | |
| 2021 | 小問集合 マーク式 | 集合・命題と不等式 マーク式 | 確率 マーク式 | 2次曲線 (1)~(5)のうち、(5)のみ記述式 | |
| 理工共テ併用 | 2025 | 解けない漸化式と評価 記述式 | 小問集合(集合・命題アリ) マーク式 | 点光源(影の面積の最大・最小) マーク式 | |
| 2024 | 小問集合 マーク式 | 数列(帰納法) 記述式 | 平面ベクトル マーク式 | ||
| 2023 | 小問集合(集合・命題アリ) マーク式 | 逆関数のグラフと面積 マーク式 | 定積分数列と帰納法 記述式 | ||
| 2022 | 小問集合(集合・命題アリ) マーク式 | 空間座標 マーク式 | 複素数と数列 マーク式 | 軌跡と直線の通過領域 記述式 | |
| 2021 | 媒介変数表示と2次曲線 マーク式 | 小問集合(集合・命題アリ) マーク式 | 複素数平面(1の5乗根) マーク式 | ベクトル(立方体)とⅢのグラフ (1)~(3)のうち、(3)のみ記述式 |
マークのさせ方
前項の表からも分かる通り、解答形式は、
- 文系はほぼマーク式
- 理系は7割方がマーク式
です。マーク式の怖さについては↓の記事を、


マーク式テストに対する準備については↓の記事を、


併せてご参照くださいm(_ _)m
後者の記事に則り、上智大学の数学のマークのさせ方を確認しておきましょう↓
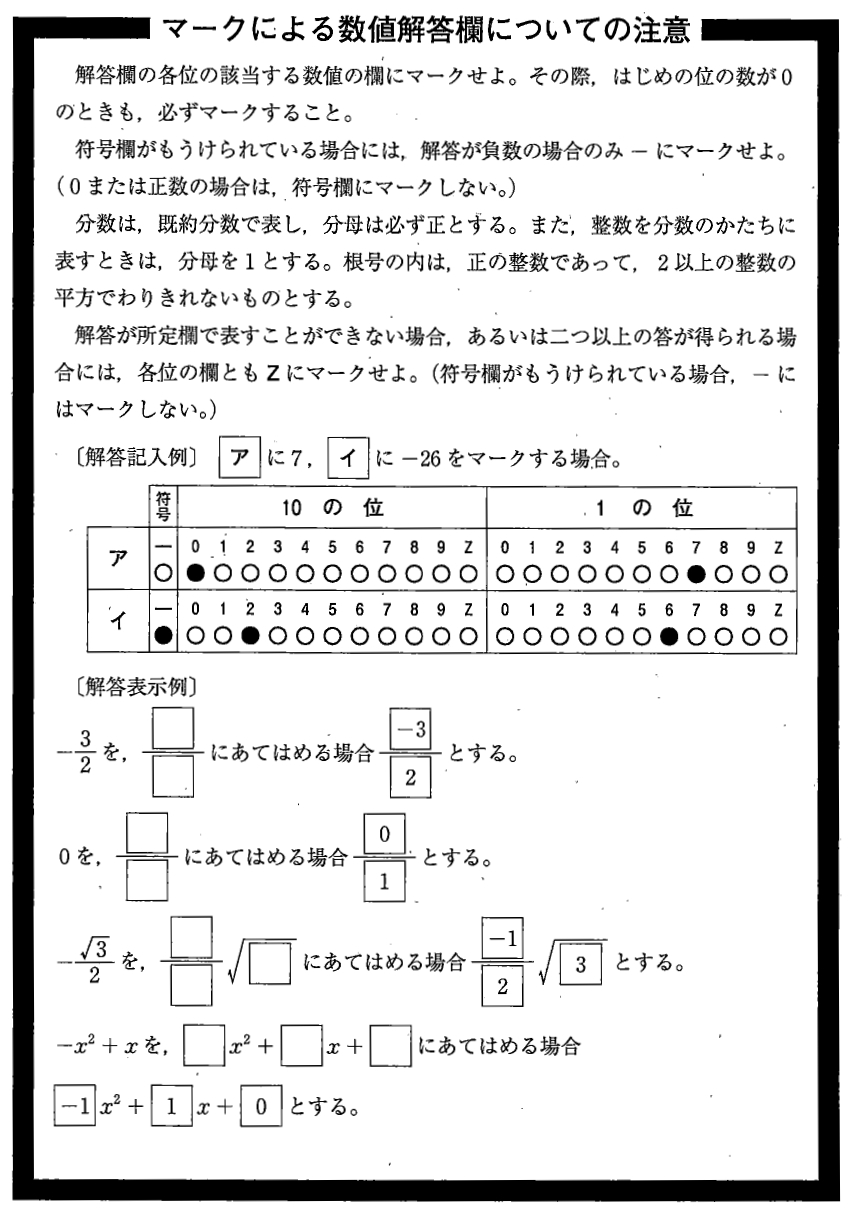

カタカナ空欄は、\(-99\) ~ \(99\) の整数値をマーク、当てはまらない場合はzをマークする
が基本で、
zをマークすることは(ほぼ)ない!



文理共通で、マークのさせ方は↑が基本となります。他大と違って、当てカンでは当たりにくいです(笑)
因みにzマークを「ほぼ」ない、としたのは2023文系TEAP利用の上智大学の公式解答がzマークも許容していたからですが、基本zマークは有り得ないと考えて良いと思います。
他にも、
- ひらかな空欄には、アルファベットをマーク
- 3ケタ解答になる場合には、百の位のマーク欄が増設
されるようです、実際のマークシートの現物が公表されていないので、確証がなくて申し訳ないんですがm(_ _)m
他大に比べてマークが特殊であることは、事前に知っておいた方が良いでしょう。
「集合・命題」の出題
前々項の表から、近年の上智大の数学では、文理問わず「集合・命題」の内容が良く出題されていることが分かるでしょう。



皆キライだよね、安心して!プロの僕もキライ(笑)
まず、↓のような基礎事項をおさえておくことはマストになります。
「集合・命題」の基礎事項
- 集合 \(A\)={要素|要素の満たす条件} → 後ろを読んでればオッケー
- \(a\in A\) → \(a\) は集合 \(A\) の要素
- \(B\subset A\) → \(B\) は \(A\) の部分集合
- \(\overline{A}\) → \(A\) の補集合・\(A\) の否定・\(A\) ではないところ
- \(\cup\) は「または」 、 \(\cap\) は「かつ」
- \(p\Rightarrow q\) → \(p\) は \(q\) の十分条件、\(q\) は \(p\) の必要条件(矢印の向きに注目して「十発必着」って暗記するのがオススメ)
- \(p\Rightarrow q\) の対偶が \(\overline{q}\Rightarrow\overline{p}\) で、真・偽が一致
- \(\overline{A\cup B}=\overline{A}\cap\overline{B}\) 、\(\overline{A\cap B}=\overline{A}\cup\overline{B}\) → バーは分割すると「または」と「かつ」が逆転(ド・モルガンの法則)
その上で、
集合・命題の出題は、似た形で出題されていない!
ことを覚えておいてください。2023で言っても、
- 文系TEAP利用4(1)・(2) → 見た目ムズくするために使われてるだけでカンタン
- 理工共テ併用1(2) → 全部当てるのキツい、ちょっと捨て問
って感じで全く扱いが違います。2021まで遡っても、全然問題のタイプに統一感はありません。
- 「集合・命題」が頻出であることを知っておき、本番で出題されてもビビらないこと
- 小問集合での出題がほとんどなので、外してもオッケーって気持ちで時間を使いすぎないこと
- マークで出題されるから、当てカンでも埋めること
を心がければオッケーです。「集合・命題」の出題だけ解きまくって過去問対策しても、似た形で出ないんでコスパは悪いと思います。
文系数学のアドバイス
形式
| 種類 | 解答方式 | 試験時間 | 大問数 |
|---|---|---|---|
| 文系TEAP利用 | マーク式 | 90分 | 3~4問 |
| 経済共テ併用 | ほぼマーク式 | 75分 | 3問 |



2021~2025は↑の形式です。文系TEAP利用は2024だけ大問数が3問でした。2026以降も大体この感じでの出題だと思って良いでしょう。
大問1つに20分以上使える、国公立大学の数学と同じような構成になっています。ただし、記述式の国公立大学の数学とは異なり「ほぼマーク式」なので、計算ミスが怖いテストであることは理解しておいてください。
大問の難易度差が激しい
GMARCHの文系数学と比べると、受験生が既視感を覚えないような作問が多く見られます。そのため、
大問の難易度差が激し~
と思う受験生が多いでしょう。



こ~ゆ~問題で「見た目のムズさに惑わされないようにする」とかゆー対策を身につけるも重要なことは…
典型問題を確実に得点すること!
です。どのセットでも、超典型的な大問が1つは存在します。これを見つけて、取りこぼさないことを最優先にしましょう!
| 種類 | 年度 | 超典型的な大問 |
|---|---|---|
| 文系TEAP利用 | 2025 | 1 |
| 2024 | 1 | |
| 2023 | 1 | |
| 2022 | 2・3 | |
| 2021 | 2 | |
| 経済共テ併用 | 2025 | 1 |
| 2024 | 2・3 | |
| 2023 | 2・3 | |
| 2022 | 2 | |
| 2021 | 3 |
「面積」の出題頻度が高い
「2次関数・3次関数のグラフの面積」が高い頻度で出題されています。
面積公式(3次まで)
\(\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx\)\(\:=\displaystyle\frac{1}{6}(\beta-\alpha)^3\)
\(\displaystyle\int_{\alpha}^{\beta}(x-\alpha)^2(x-\beta)dx\)\(\:=-\displaystyle\frac{1}{12}(\beta-\alpha)^4\)
\(\displaystyle\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)^2dx\)\(\:=\displaystyle\frac{1}{12}(\beta-\alpha)^4\)



これらをただ暗記するのではなく、その存在理由と導出である…
代入計算を簡略化するために、共有点が絡む面積では0になる因数基準で計算する、というところまで理解していないと、対応が難しい問題がほとんどです。この意味が分からない人は、めぐろ塾↓への入塾を検討した方がいいかもしれない(笑)


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
「ベクトル」は「空間」で出題されている
GMARCHの文系数学では「ベクトル」は「平面」で出題されることがほとんどですが、上智の文系数学では「空間」で出題されることがほとんどです。



2022経済共テ併用では「空間座標」(ベクトルの利用)まで出題されています。この部分はかなり早慶の文系数学に近いです。
文系だと「ベクトル」の勉強が「平面」までで止まってしまっている人も多いのではないでしょうか?上智だと「空間」までの「ベクトル」の勉強は必須です。
因みに理系まで見ると「立方体」での出題が多いので、対策としては理系の問題を解いておくのもいいかもしれません、立方体の図の使い回しも見られたので(笑)理工TEAP利用の2022の2・2023の3なんかは理系専用範囲の知識は使わないので、解いておくのがオススメです。
理系数学のアドバイス
形式
「TEAP利用」・「共テ併用」共に、
| 解答方式 | 試験時間 | 大問数 |
|---|---|---|
| 大問3つはマーク式、 1つだけ記述式 | 90分 | 4問 |



がベースと思っておきましょう。2024TEAP利用は記述式が2つ、また
2023~2025共テ併用は大問が3つになったりと、多少の変化はありますが。
問題を解く順番
ほぼ全てのセットで、「小問集合が1題、記述式の大問が1題」は含まれています。
カンタンな問題はすんごくカンタンです。ここの点数をまず確保しましょう。
部分点がもらえるから!時間はかけすぎないこと!
満点はムリなセットがほとんどです。全部完璧に解こうとしないこと。でも、特に「集合・命題」とかは当てカンでも埋めること。



試験本番では、この順↑で解くのがオススメです。
理科大より解きにくい
冒頭でも話した通り、理系では「上智理工≒東京理科大」なので、併願する人も多いでしょう。



僕も併願したんですけどね、全然上智の数学の方がムズく感じました。
理科大が典型問題ベースで出題するのに対し、上智の数学が、他大であまり頻出ではない内容を出題してくるからです。2023~2025で言えば、
- 2025理工TEAP利用3の水量問題
- 2025理工共テ併用3の点光源
- 2024理工TEAP利用4の3項間漸化式と証明
- 2024理工共テ併用のビリヤード
- 2023理工TEAP利用3の水量問題
- 2023理工共テ併用2の逆関数のグラフの求積
などがこれに当たります。
その中でも特に歴史的に気になるのが…
「極座標」からの出題
他大はホントに出題してこない範囲です。直近では、2022理工TEAP利用の4↓で出題されています。


極座標きたぁああああああああああー!
終わったぁああああああああああああああああああああああああああー!



って思っちゃって終了しちゃった人、一定数いると思うんですよね…
極座標の知識なんてほぼ使いません!
三角関数の定義から、\(\begin{equation}\begin{cases}x=r\cos\theta\\y=r\sin\theta\end{cases} \end{equation}\)
↓
\(r=1+t\) と \(\theta=\log(1+t)\) を代入して、
媒介変数表示 \(\begin{equation}\begin{cases}x=(1+t)\cos\{\log(1+t)\}\\y=(1+t)\sin\{\log(1+t)\}\end{cases} \end{equation}\) を立式
として、他大でも頻出の「媒介変数表示された曲線」の問題と考えるだけです。



この問題はまだマシな方。↓は上智理工を受けるなら絶対に解いておいた方が良い問題です。
2018理工(一般)4
問題
4問題①-1.jpg)
4問題①-1.jpg)
4問題②-1.jpg)
4問題②-1.jpg)



やはり90分大問4つの中の1つとして出題された問題です。25分くらいで解いてみてください!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
考え方
(2)以降の流れは、
陽関数に変更しても解析できないレベルの陰関数表示で表された曲線 \(C\)
↓
極座標 \(r=f(\theta)\) に変換
↓
解析可能な媒介変数表示 \(\begin{equation}\begin{cases}x=f(\theta)\cos\theta\\y=f(\theta)\sin\theta\end{cases} \end{equation}\) を立式
となっており、特に陰関数表示を極座標に変換する部分は、他大では頻出と言えません。



20年のキャリアで、2018東京医科大5しか経験がありません。これは極座標の誘導もなく、最悪の出題でした(笑)
(1)から「レム二スケート曲線だ~」なんて思える人はほとんどいないでしょう、気づいていてもほぼ意味はありません。
この問題で解けて欲しいのは(2)~(5)!
(1)は、\(\textrm{P}\:(x\:,\:y)\) とおいてPA・PBを計算、与方程式を使って式を簡略化し、\(x\:,\:y\) の恒等式にするだけですが、計算が複雑です。解けなくて良いんで、諦めずに(2)に臨んでください!
(2)は極座標の知識なんてほとんどいりません!三角関数の定義から、\(\begin{equation}\begin{cases}x=r\cos\theta\\y=r\sin\theta\end{cases} \end{equation}\) を代入して、ノリで当てましょう!
(3)が一番の鬼門です!やはり極座標の知識なんて使いません!最初の \(C\) の陰関数表示から、
- \(x\) と \(y\) を入れ替えても変わらないから \(y=x\) 対称である
- 原点を通る
ことからFとするだけ。
(4)は、(2)から \(r\) が \(\theta\) で表せるので、冒頭でも言った通り \(C\) の媒介変数表示を立式します。解答では一応断りましたが、マーク式なんでルートの中≧0とかを詳しく考察する必要はありません。「(3)から第1象限に注目でしょ~」って思って \(0<\theta<\displaystyle\frac{\pi}{2}\) で考えときましょう。これさえできれば頻出内容。媒介変数表示の図示よろしく、\(x\) の増減(グラフの横の動き)を考えるだけです。
(5)も同様に、頻出内容である「媒介変数表示で表された曲線の面積」を考えるだけ。



(2)~(5)まで、ほとんど皆キライな「極座標」の知識は使いませんでしたね!
見慣れない問題に出会ったときに重要なのは、
自分の知ってる知識で何とかしようとすること!
特に上智理工の数学は、他の問題でもこういった能力を要求してくることが多いです。



(6)は解けなくてオッケー!
(5)と同様に、頻出内容である「媒介変数表示で表された曲線の面積」と考えて解くことも可能ですが、\(y\) 座標の区別とかが入るので時間内解答は厳しいです。時間内に当てたいのであれば、解答のように「極方程式のグラフと面積」で使える「扇形分割」を使う必要があります。これはそもそも裏ワザ扱いで記述式で使っちゃダメとされている、かつ極座標のそこそこ深い知識と言えるので、外しちゃって良いでしょう。
でも…(5)の結果を正しく \(\displaystyle\frac{1}{16}\) って計算できてたら…
整数マークだから(3)の図からして大体1じゃね?
って当てカンして欲しいかも(笑)それが正解です!
解答
4解答①.jpg)
4解答①.jpg)
4解答②-1.jpg)
4解答②-1.jpg)
まとめ



上智大学の数学は、文系も理系も結構特殊!
ってのがまとめになっちゃいますかね(笑)
他大よりも、過去問対策の重要度が高いと言えるでしょう。文系で言えば早稲田社学、理系で言えば理科大や早稲田理工なんかは記述部分が多くてあんまり過去問対策いらないんですが、過去問対策なしで上智の数学受けるとメンタルをやられてしまう可能性があります(笑)
しっかり準備をして臨んでください!この記事がその助けになれば幸いですm(_ _)m
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!


















