2026慶應商【数学】解答速報
2026慶應義塾大学商学部の数学の解答速報をお届けします！
めぐろ塾の安田人員不足のため、一人で孤独にやっております(笑)
ミスを見つけた方は、X（Twitter）のDM等でご指摘頂けますと幸いですm(_ _)m
Ⅰ
問題
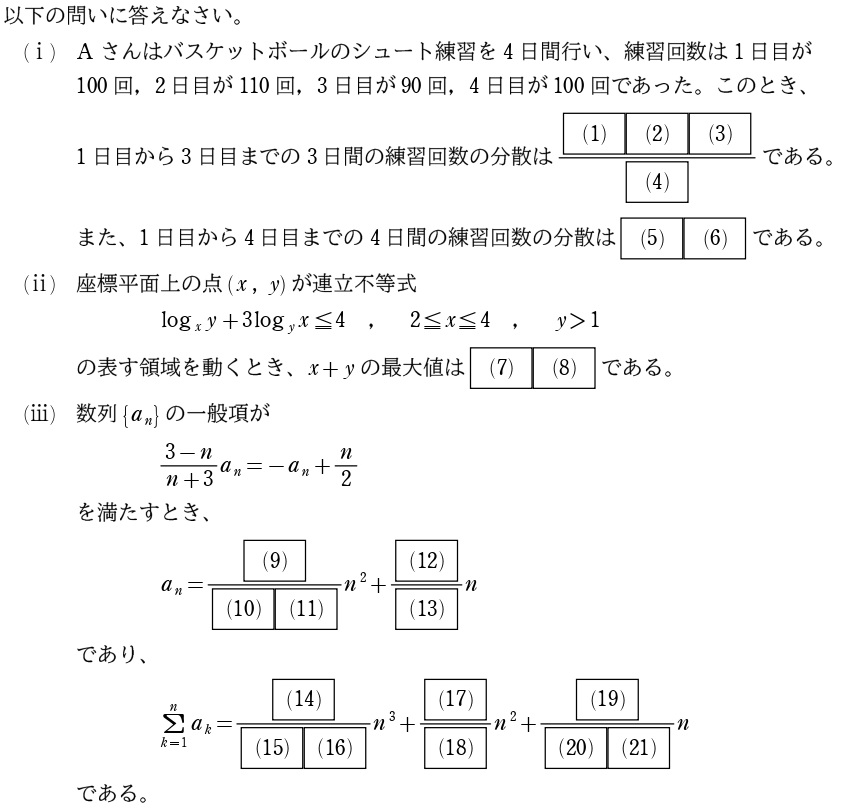
考え方
今年も小問集合からスタート、昨年と同じくカンタンな問題ばかりでした。
(ⅰ)は分散の計算ですが、平均がどっちも100になるのでほぼ暗算できるレベル。
めぐろ塾の安田解答では義務感で表に偏差とかまとめときましたが、実際全く必要ないです(笑)
(ⅱ)は領域を図示して、\(x+y=k\) と共有点を持つって考えるだけ。対数不等式は底を \(x\) にそろえるとlogの積商形になるので、置き換えの意識で整理しましょう。
(ⅲ)は最初漸化式と見間違えてしまいました…何と \(a_n\) がただの１次方程式で表されているだけなので、整理して一般項を求めるだけ…シグマ計算も公式使うだけで教科書レベル。
(ⅳ)は必要・十分条件の判定。条件を同値変形で \(x\) について整理し、冷静に読み取りましょう。解答では義務感で反例とか示しましたが、全て包含の意識で判定できるレベルです。
(ⅴ)は３倍角の公式使っとけばただの３次方程式解くだけの問題。
めぐろ塾の安田カンタンな問題ばかりなので、何とか計算ミス１つとかで切り抜けたい。
解答
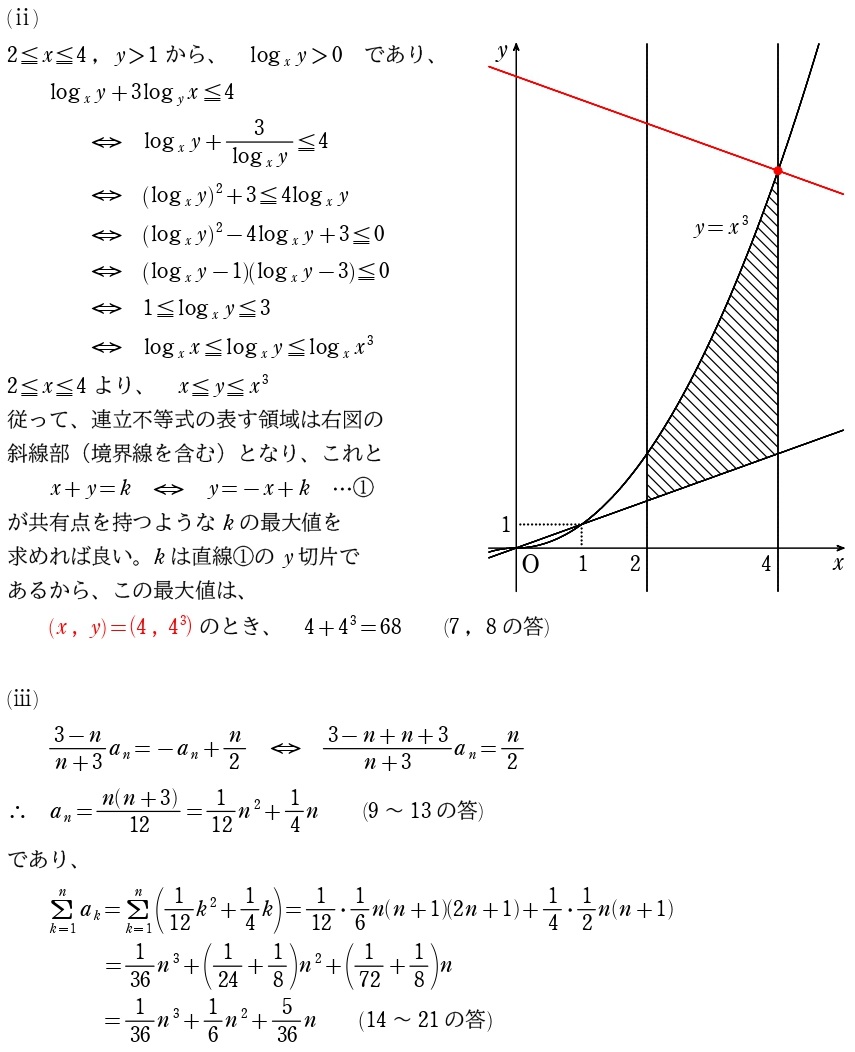
Ⅱ
問題
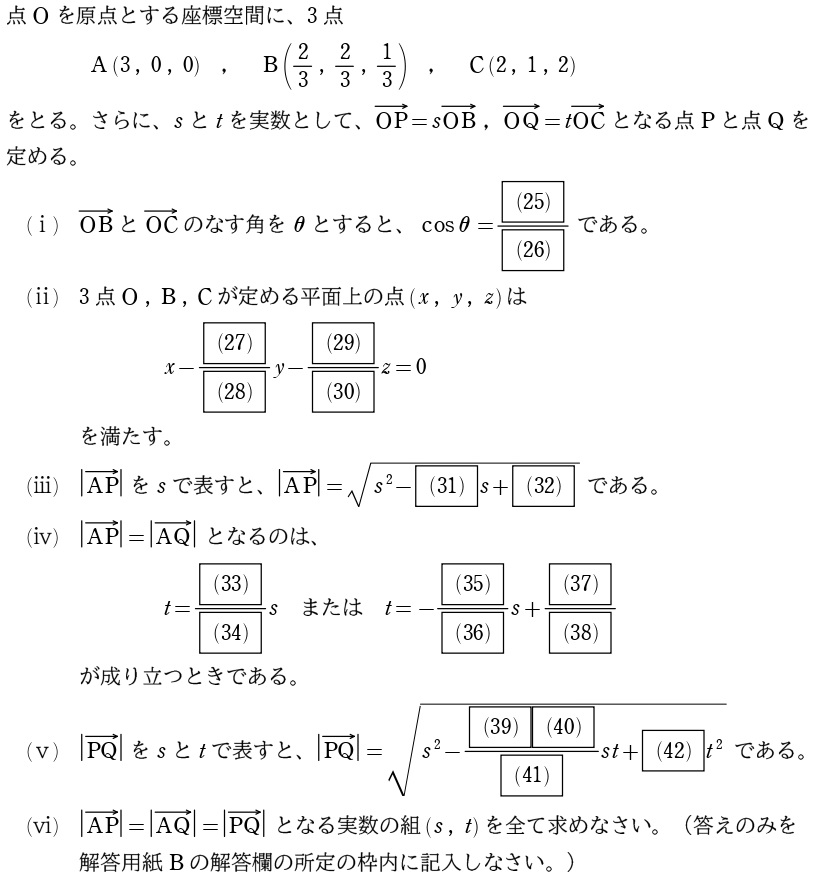
考え方
(ⅰ)は内積使ってるだけ。
めぐろ塾の安田(ⅱ)は平面の方程式の一般形の立式。意外と受験者の出来は悪いかと思います。めぐろ塾↓では授業でやらせてます、的中！！！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
授業では、平面を媒介変数表示させるのを徹底しているので、これで立式しましたが、法線ベクトルを使って立式しても良いでしょう。
(ⅲ)～(ⅴ)はただの大きさ計算。そして…
めぐろ塾の安田個人的には(ⅵ)がイヤでした…最終結果もめっちゃ汚くなったんすけど…３回計算ミス確認して見つからなかったので…一応これを答としておきます(笑)
設問の流れを考えると、解答のように大きさ条件で処理するべきかと思いますが…
- ってか結局(ⅱ)は使わないの？って思っちゃう
- 正三角形作れってことだから、挟角の処理とかしたくなっちゃう
問題…
めぐろ塾の安田ま～計算もそこそこ複雑だし、最後の設問だし、(ⅴ)は外しちゃっても良いでしょう。
解答
Ⅲ
問題
考え方
めぐろ塾の安田本校受験者に解説とかいらないだろ…これ…(笑)
グラフと積分の極めて基本的な内容です。注意するのは、
- \(y=f(x)\) と \(y=g(x)\) は \(x=4\) で接するので、\(f(x)-g(x)\) は \((x-4)^2\) で因数分解できる
- (ⅲ)ではそれを意識し、\((x-4)\) 基準で計算する（１／６公式の導出と同様）
とこだけです。面積計算でもないので、全体的にグラフの図示も不要で解けてしまう問題です。
解答
Ⅳ
問題
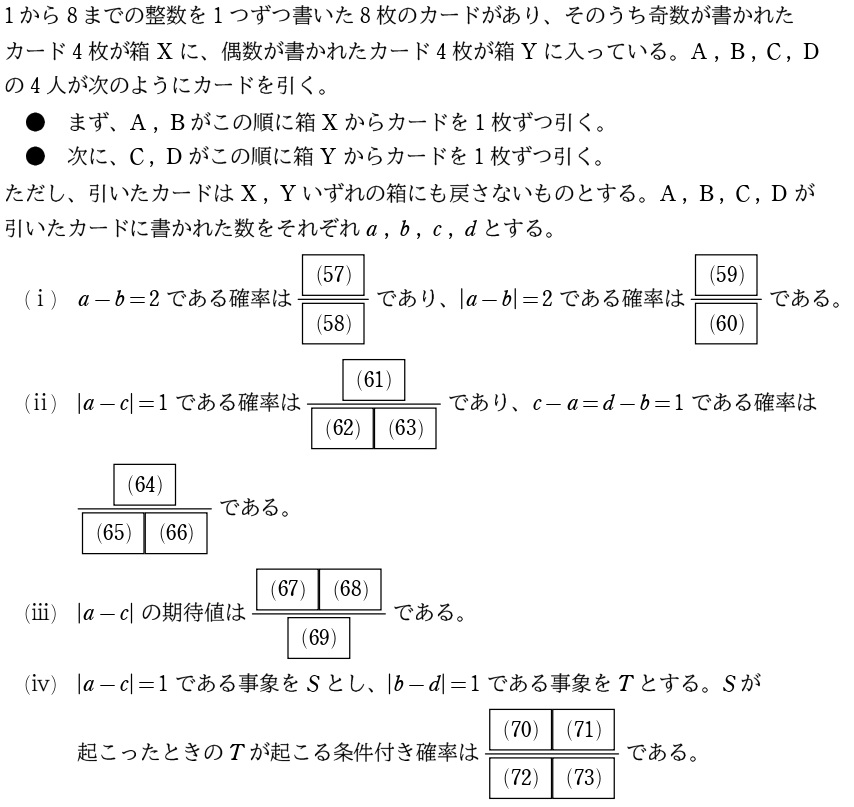
考え方
めぐろ塾の安田今年の慈恵会医科大の最初も絶対値の確率だったので、似てて少しびっくりしました(笑)
全体的に数えていくだけの確率の問題！
…だと思います…確率ニガテなんで自信はないですが(笑)
最後の(ⅳ)は個人的に苦しみました。ど～数えるのがベストなのか良く分からなくて。例えば奇数２つ（\(a\:,\:c\)）を決めて考えようとしても…
- ３と５とか連続する奇数だと、偶数の決め方は \({}_3C_2\) 通り
- でも、１と３の場合だと１通り
- ３と７とかだと４通り
ってことであんま上手くいかない…
試験中なら上手く数えようとせず、しらみ潰しちゃった方がいいと思います。しょせん、奇数の選び方は \({}_4C_2=6\) 通りしかないので。
めぐろ塾の安田でも僕は解答打たないといけないから…
30分悩んで作った解答では偶奇のペアの作り方に注目させて頂きましたが…
これもそんなにキレイな解答ではないですね(笑)
※追記
一回寝たら、解答の数えてる15通りは、(〇〇)＝△：２個と〇：４個の並べ方で \({}_6C_2=15\) 通りと計算できることに気づきましたが…記述しにくいので、解答は直さないでおきます(笑)
ま～最後は外しちゃっても良いでしょう。
なお、(ⅲ)は \(|a-c|=3\) 辺りは余事象を使って計算した方が良い気もしましたが、計算ミスの確認の意味合いで、全ての場合を直接計算しています。悪しからずご了承くださいm(_ _)m
解答
講評
昨年2025も解答速報↓
を行いましたが、これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| マーク式、 一部答のみ解答 | 70分 | ４問 | やや易化 |
です。
めぐろ塾の安田個人的にはⅡの最後の計算で悩んだり、Ⅳの最後の解答の書き方で悩んだりしたんでやや難化なんですが(笑)
過去最高レベルにカンタンだった2025よりも、
- 基本問題が増えた
- 大問もとっつきにくいのがない（去年はⅢは苦しんだ人が多かった気がする）
ので、やや易化が妥当かと思います。
めぐろ塾の安田いかにミスを減らせるかが勝負のテスト！
だったでしょう。合格者平均とかはかなり高得点になりそうな気がします…
でも…
数学ヤバかったぁあああああああああああああああああああー！！！
めぐろ塾の安田って人も凹むな！社会利用に比べて数学利用の合格最低点はいっつも凄く低い！！他の科目次第でワンチャンあるぞっ！！！
ってか終わったテストは引きずらないように。
早慶のうち、早稲田の入試が控えてるぞっ！！
それに向けて勉強頑張って！！！
めぐろ塾の安田上智→慶應の解答速報で疲れてきた僕も、来週は早稲田地獄…
大丈夫、君は一人じゃない(笑)
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
