「平均値の定理」を徹底解説!

「平均値の定理」覚えらんねぇえええええええええええええええええー!!!
って理系の高校生に…
 めぐろ塾の安田
めぐろ塾の安田指導歴20年、現役で早稲田理工なのに現役時「平均値の定理」がビミョーだった私めが…
「平均値の定理」を徹底的に解説して差し上げます!!
結論:グラフからすれば当たり前!



↓のグラフの状態だけ覚えておけばオッケー!
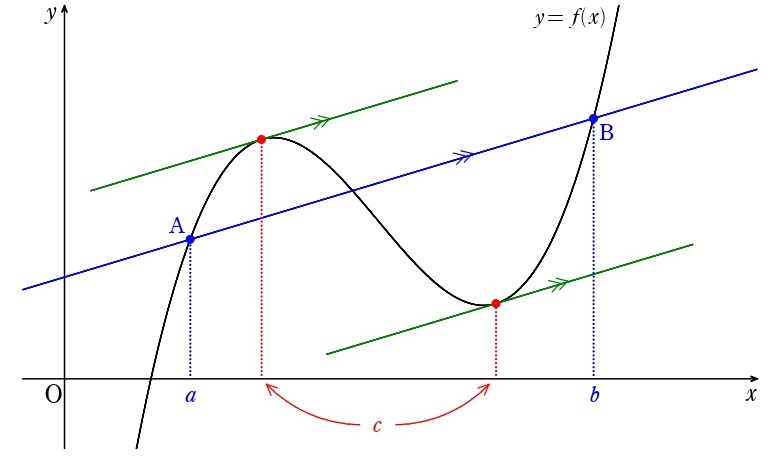

グラフ上の2点 A、Bを結ぶ直線と平行な接線が、
AB間に引ける
A\((a\:,\:f(a))\) 、B\((b\:,\:f(b))\) より、直線ABの傾きは \(\displaystyle\frac{f(b)-f(a)}{b-a}\) です。接線の傾きを求めるための演算が「微分」であることを意識すると…
解答への書き方(端の大小確定バージョン)





端(\(a\:,\:b\))の大小が確定している場合はこれ↑でいいんだけど…
解答への書き方(端の大小分からないバージョン)





端(\(a\:,\:b\))の大小が分からないときは、↑のように記述するクセをつけておきましょう!
こだわりたい人向け



少々マニアックな話になるので、次項に進んで構いません。
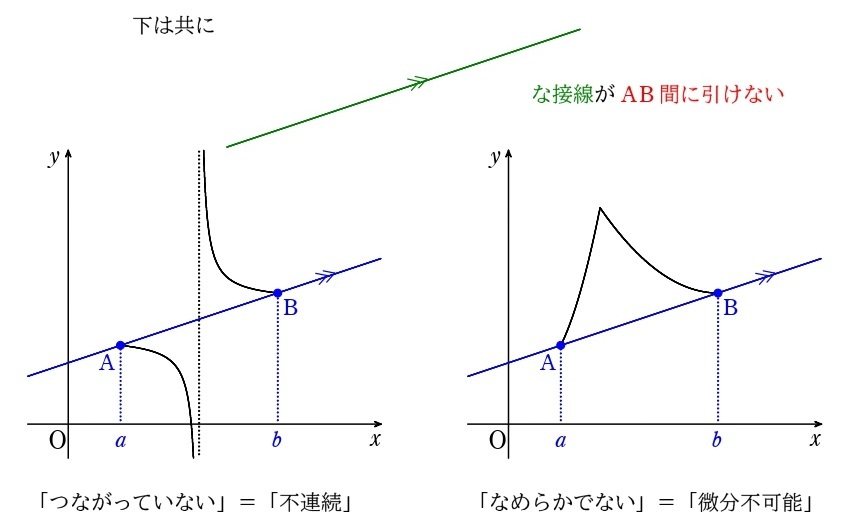

ことが分かるでしょう。なので、ホントに厳密に「平均値の定理」を使うのであれば、
\(y=f(x)\) が \(a\) から \(b\) で「連続」かつ「微分可能」であることを断る
必要があります。



なんだけど…ウゼーことにここで…
ってことで…
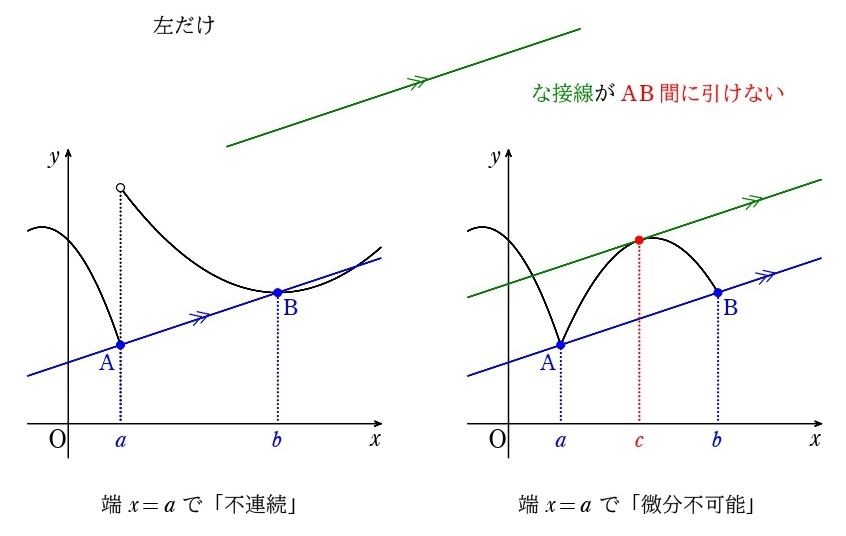

- 「連続」は閉区間 \(a≦x≦b\)(カッコよく書くと \([a\:,\:b]\))で断る
- 「微分可能」は開区間 \(a<x<b\)(カッコよく書くと \((a\:,\:b)\))で断る
必要が出てくるってゆ~…



僕は一応プロとしての義務感で暗記してますが…
「生徒にここまで意識させる必要あるか?」って気がするので…
全体で「なめらか」に「つながっている」なら…
↓
一部分でも「なめらか」に「つながっている」に決まってる!
ってことで、余力のある生徒には↓のように記述するよう、めぐろ塾では指導しています。





↑は「端の大小分からないバージョン」で書いたので、「端の大小確定バージョン」で具体例を示します↓\(f(x)=\log x\) の場合であれば…


因みに、\(y=f(x)\) がどんな関数であろうが、「平均値の定理」を使うときにイメージするグラフは最初に提示した3次関数チックなグラフで大丈夫です。



「なめらか」に「つながっている」グラフでは絶対に成立する定理なので。僕は常に頭の中で3次関数チックなグラフをイメージする、って決めています。
ま~一応プロとしての義務感で説明しましたが…
本項の内容はおさえなくても大丈夫です。



ほとんどの解答、「平均値の定理」を使うときに連続と微分可能は断ってないんですよね…10年前くらいまでは自分のプリントにしっかり記述してたんですけど、記述しない解答に打ち直しました(笑)
使用ケース
平均値の定理の等式は、


等式です。なので本質的に「平均値の定理」の使用ケースをまとめると…
「平均値の定理」の使用ケース
「変数の差」と「関数の差」が式中に登場
↓
「平均値の定理」を利用
ってなるんですが…



これだとざっくりし過ぎてて、どのタイプの問題で使うのか迷っちゃうよね(笑)
式をシンプル化してくれる定理だから、色んなケースで使えちゃう。
これが「平均値の定理」の難しいところです。この記事では対象にしませんが、不等式証明で楽するために使うこともあります。
なので…
実践的な使用ケース
大学受験で絶対に「平均値の定理」に気づけないといけないケースについては暗記しちゃいましょう!
極限計算



あんまり出題されていません(笑)
でも「平均値の定理」の練習って意味では経験しておくと良い問題でしょう。
問題
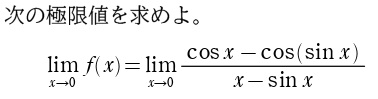
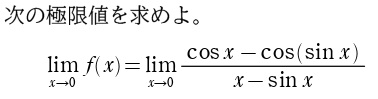


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解説・解答



代入すると \(\displaystyle\frac{0}{0}\) の不定形になりますが、公式 \(\displaystyle\lim_{x\to 0}\displaystyle\frac{\sin x}{x}=0\) やはさみうちの原理で計算できない形です。分母に「変数の差」・分子に「関数の差」があることから、「平均値の定理」の利用に気づきましょう。問題文にわざと \(f(x)\) を使って解答を書きにくくしておきました(笑) \(g(x)\) 辺りを使って、これと端に当たるものを読み取りましょう。常に↓のようにグラフをイメージするのがオススメです。
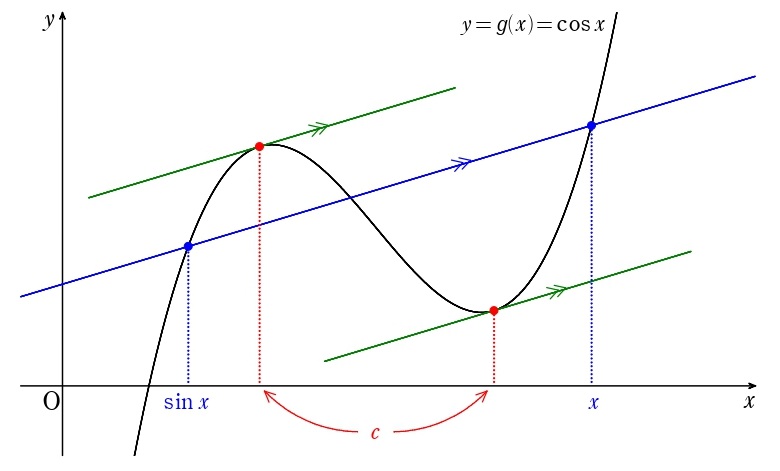




全然 \(y=\cos x\) は↑の形じゃないですけどね(笑)
なめらかにつながってるグラフなら絶対に成立するのが「平均値の定理」なんで、形なんてどーでもいいです。端に当たる \(x\:,\:\sin x\) の大小は0の前後で切り替わるので、端の大小分からないバージョンでいきましょう↓





これで \(\displaystyle\lim_{x\to 0}f(x)=\displaystyle\lim_{x\to 0}(-\sin c)\) と計算対象をシンプルに書き換えられましたが、書き換え後が \(c\) の式なので、\(c\) の飛ぶ場所を求めなければなりません。\(c\) が、\(x\) と \(\sin x\) の間であることから、「はさみうちの原理」を利用します。
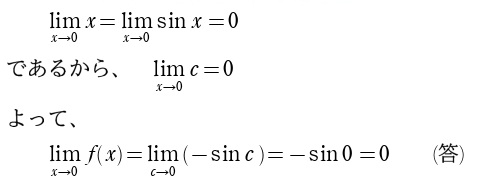
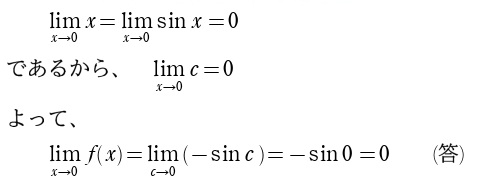
東京医科問題
2013で出題時、医学部専門予備校界隈ではそこそこ話題になった問題です。



他大ではほとんど目にしないんですが…東京医科はホントに記述専用的な知識をマーク式の問題に落とし込む作問が上手い…
「平均値の定理」に気づきにくい問題です。
僕も当時解いてて5分くらいフリーズしたから、試験時間内じゃ厳しかったかも(笑)
同様の問題が2020でも2題出題されており、東京医科大を受験する生徒は対策必須な問題です。
東京医科大で「不等式と整数」の問題が出題
↓
「平均値の定理」じゃね?



って思えるようにしておいて欲しいくらい。
そろそろ出題されるかもよ?(笑)
問題


解説・解答



与不等式の左辺に「関数の差」が登場していますが、「変数の差」\((n+9)-(n+8)=1\) が分母にあるって気づくのが難しい=「平均値の定理」の利用に気づきにくい問題です。因みにイマイチ十分性が曖昧になるので、最後に断りを入れてますが、マーク式なのでこの部分は気にしなくていいです、ただのプロとしてのプライド(笑)


解けない漸化式と極限~応用型~
受験数学における、
「平均値の定理」の存在理由は、この問題のため



と言ってしまって良いくらい、上位校での典型問題です。
知ってなきゃ絶対解けない(笑)
解けない漸化式 \(a_{n+1}=f(a_n)\) と極限の問題は…
\(\displaystyle\lim_{n\to\infty}a_n=\alpha\) とすると、
\(\alpha=f(\alpha)\)
で、
漸化不等式 \(|a_{n+1}-\alpha|<●|a_n-\alpha|\)
ただし、\(0<●<1\)
を作るのが大事!
って法律を知らない人は↓の記事をご覧くださいm(_ _)m


↑の記事で紹介している、分数型・ルート型(紹介してませんが整式型も)の漸化式であれば式変形で漸化不等式を作れるんですが…


というように、指数型・三角関数型の漸化式だと式変形では漸化不等式が作れないんですよね…
でも…





ってことになる…
知らなきゃ絶対ムリだろ、こんなの(笑)
因みに、分数型・ルート型・整式型の漸化式も「平均値の定理」で漸化不等式を作れるんですが、これらは式変形で作るようにしてください。



採点者側からすると式変形の解答を想定しているので、採点しててちょっとイヤになるから(笑)
それでは…
1問用意したんで解いてみましょう↓2013日大医学部をカンタンにした問題です。
問題
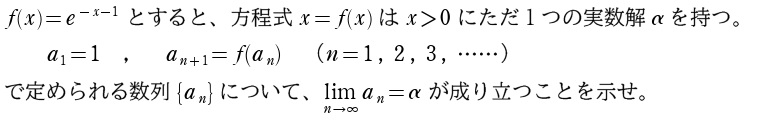
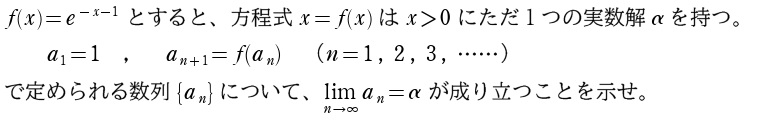


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解説・解答



「平均値の定理」の利用に気づいたら、取りあえず \(a_n\) と \(\alpha\)(極限値)で平均値の定理を使っちゃうのがオススメです。後は \(\alpha=f(\alpha)\) を唱えてれば何とかなる(笑)





\(e^{-c-1}\) を評価して、漸化不等式を完成させましょう。\(c>0\) を使えば \(●=\displaystyle\frac{1}{e}\) で \(0<●<1\) となり成功です。\(c\) は「\(a_n\) と \(\alpha\) の間」だから、\(a_n>0\) と \(\alpha>0\) を言えばオッケー! \(\alpha>0\) は問題文から明らかですが、\(a_n>0\) は断るべきで、厳密には帰納法で証明するので「帰納的に」って言葉を入れておくとベストです。





漸化不等式が完成したので、繰り返し使ってはさみうちの原理を使えば証明終了です。↑の評価の詳細で混乱しちゃった人も、当てカンで \(\displaystyle\frac{1}{e}\) 辺りを使って強引に漸化不等式を立ててしまい、↓の過程は書きましょう。部分点はもらえるはず(笑)





この記事の趣旨からは外れるので削除しましたが、実際は「\(x=f(x)\) がただ1つの実数解を持つ」ことも証明対象でした。しかも(2)での評価を見越して、「\(x>0\) に」って部分は自分で見抜かないといけないし…それでも15分くらいしか使えないし…(笑)
大学受験の厳しさを認識してくださいm(_ _)m
まとめ



「平均値の定理」なんて、グラフからすれば当たり前!
すこ~し、数学的な言葉に変換するだけです。



こんなカンタンな定理をおさえていないのはもったいない!
「平均値の定理」が受験時ビミョーで…



受けた大学で出題されなくて良かった~
って思ってる恥ずかしい大人にならないよう、皆さんはしっかり受験時におさえてください(笑)
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!







