解けない漸化式と極限


 めぐろ塾の安田
めぐろ塾の安田この問題↑は2021信州大の問題ですが…理系の人は問題集とかで似た問題を目にしたことがあると思います。この問題で…こんな↓
- なんで数列から3が引かれてんねん…
- なんで絶対値がついてんねん…
- 全体的に意味不明…
を持っている人もいるんじゃないでしょうか?この記事では、こんな疑問を徹底的に解消して差し上げますm(_ _)m
結論:ほぼほぼ解き方を暗記しておくべき



冒頭で紹介した問題…大学受験の典型問題の中でも、メッチャ難しい問題の1つです…でも…
受験で大事なのは難易度よりも頻出性
めぐろ塾の解答速報で書いている2023~2025だけで言っても、
で出題されており、1年に上位校で1回程度は出題されている頻出内容と言えます。



マイナーな処理が必要な問題は、解けなくても凹む必要はありません。
受験で大事なのは、頻出問題を確実に解答すること
↓
この類問が出題されて、全く手が出ないのはアウト!
です。そして…
類問経験がない人が初見で解くのはムリ



です、このタイプの問題は…天才さんじゃない限り。
この後の解説を見ても痛感できると思います。頻出性を認識し、ほぼほぼ解法を暗記するように努めてください。
誘導ナシで解けるようにしよう!
冒頭で紹介した通り、このタイプの問題は誘導アリで出題されることが多いんですが、全く誘導ナシで出題されることもあるので、誘導ナシの場合の解法を暗記した方がいいです。



誘導アリの場合、「逆に解きにくい」ってなるのが理想。とゆ~わけで一問用意しました↓
問題
.jpg)
.jpg)
この漸化式は解けない



少々マニアックな話になるので、次項に進んでしまって構いません。
この問題の漸化式は「解けない」=「一般項が求められない」扱いになります、大学受験では。一応…
1次分数型漸化式と特性方程式
\(a_{n+1}=\displaystyle\frac{ra_n+s}{pa_n+q}\) について、特性方程式は \(t=\displaystyle\frac{rt+s}{pt+q}\)(\(t\) の2次方程式となる)であり、
- \(s=0\) の場合、逆数をとって \(b_n=\displaystyle\frac{1}{a_n}\) とおけば解ける
- \(s≠0\) の場合、特性方程式の2解を \(t=\alpha\:,\:\beta\) とすると、\(c_n=\displaystyle\frac{a_n-\beta}{a_n-\alpha}\) は等比数列となる
- さらに \(x_n=a_n-\alpha\)(or \(a_n-\beta\))の漸化式は①タイプになるので、逆数をとって \(y_n=\displaystyle\frac{1}{x_n}\) とおけば解ける
- さらに \(\alpha=\beta\)(特性方程式が重解を持つ)とき、\(y_n\) は等差数列となり、\(a_n\) の結果を推測可能
の②や③を知っていれば一般項は求められるんですが…大学受験では、
- 誘導ナシで一般項を求めさせる場合 → ①・④で出題(④は「推測+帰納法証明」)
- ②・③を使う場合 → 問題で誘導を与える



という紳士協定的なものがありまして(笑)
この紳士協定を破った出題もなくはない(2023昭和大医学部Ⅱ期)ですが、極めてまれです。
この問題は \(s≠0\) より①ではなく、漸化式の特性方程式は、 \(t=\displaystyle\frac{5t+9}{t+5}\)
分母を払って、 \(t^2+5t=5t+9\) ∴ \(t=±3\)
となり、特性方程式が重解を持つタイプ④でもありません。よって紳士協定から、大学受験ではこの漸化式の一般項は求められない扱いになります。
でも極限値は分かる
漸化式と極限値
漸化式 \(a_{n+1}=f(a_n)\) で定義される数列 \({a_n}\) が \(\alpha\) に収束するならば、
方程式 \(\alpha=f(\alpha)\) の解 \(\alpha\) に収束
する。
一応↑は公式化しておくべきですが、
\(\infty\) からしたら1や2なんてカスみたいなもん
↓
\(\displaystyle\lim_{n\to\infty}a_n=\alpha\) ならば…
↓
\(\displaystyle\lim_{n\to\infty}a_{n-1}=\alpha\) 、
\(\displaystyle\lim_{n\to\infty}a_{n+1}=\alpha\) 、
\(\displaystyle\lim_{n\to\infty}a_{n+2}=\alpha\) 、
大きくずれても \(\infty\) に比べたらカスで… \(\displaystyle\lim_{n\to\infty}a_{n+10000}=\alpha\)



って意識を持っていれば当たり前です。今回の漸化式で具体的に使ってみましょう。\(\displaystyle\lim_{n\to\infty}a_n=\alpha\) として…


因みに記述式の場合、これで終わりにするとほとんど点数はもらえません….



この計算は「収束する」のを前提としているので。
\(\{a_n\}\) の収束を示さないとアウトです。
よって以下、
極限が直接計算しにくい → 「はさみうちの原理」を利用
という大学受験数学の法律に基づき、これを示します。
\(\alpha=3\) に収束するのを示すのマジでムリ



3に収束する極限の公式なんてない!!!
3はムズイから、例えば…


収束値は0の方が嬉しい!
ことを意識しましょう。今 \(\displaystyle\lim_{n\to\infty}a_n=3\) なので、
\(\displaystyle\lim_{n\to\infty}\left(a_n-3\right)\)=0
の方が嬉しい!



だから誘導アリの場合の式には \(a_n-3\) とか、何かが引かれている形が登場するわけ。これで \(a_n-3\) が0に収束することを示すのが目的にできたけど…
「はさみうちの原理」で示すので、
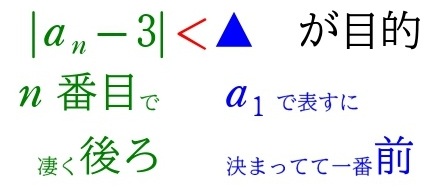
\(■<a_n-3<▲\) かつ \(\displaystyle\lim_{n\to\infty}■=\displaystyle\lim_{n\to\infty}▲=0\) が目的
↓
\(■\) か \(▲\) のどっちかは0にすると楽
ですが… \(a_n\) と \(3\) の大小比較とかダルいので…
絶対値つければいいじゃん!
\(a_n\) と \(3\) の大小比較をするまでもなく↓
\(0≦|a_n-3|\)\(\:<▲\)



とできてハッピー。だからこの系統の問題の誘導の式では絶対値がついていることが多いわけ。
因みに不等号の「=」のアリ・ナシはあまり気にしないでオッケーです。はさみうちでは「=」のアリ・ナシは結果に影響しないので。
以上から、この後の最大目標は
\(|a_n-3|<▲\) かつ \(\displaystyle\lim_{n\to\infty}▲=0\) を導く
ことになります。これを導くのに…
漸化不等式が必要
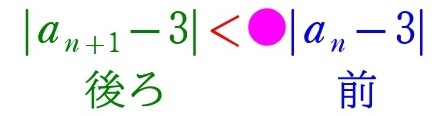
「漸化不等式」という言葉は一部の参考書では使われていますが、正式名称ではありません。これの暗記が一番大事で、大体は↓のような形になります。
漸化不等式
\(|a_{n+1}-\alpha|<●|a_n-\alpha|\)
ただし、\(0<●<1\)
今回の問題では \(\alpha=3\) なので、漸化不等式は、
\(|a_{n+1}-3|<●|a_n-3|\)
ただし、\(0<●<1\)
です。



ま~完全に暗記してないとお話しにならないんですが、理由を説明しないと暗記する気も起きないと思うので、懇切丁寧に解説します。
ここで1つ質問…
高校数学で一番解かされるのは何数列の漸化式?


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
等比数列!
って即答できなかった人は、もう少し数列の勉強をしてからこの記事を読んだ方がいいかと思います。
漸化不等式の覚え方


(等比数列の一般項)=(初項)×(公比)\({}^{n-1}\) だから…




\(|a_{n+1}-3|<●|a_n-3|\)
ただし、\(0<●<1\)
以上が今回の問題における漸化不等式の覚え方です。漸化不等式は、この後の内容も合わせて複合的に暗記するものですが、ある程度の形は覚えておかないと導きようがないので、取りあえず上のように暗記しましょう。
ここまでの解答


漸化不等式を導こう!



取りあえず漸化不等式の左辺に与漸化式を代入しましょう。通分すると勝手に右辺の形が登場します。
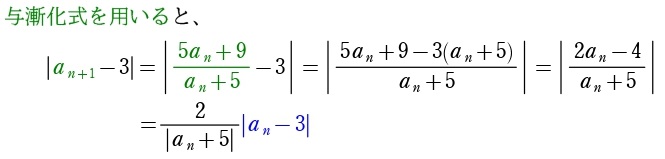
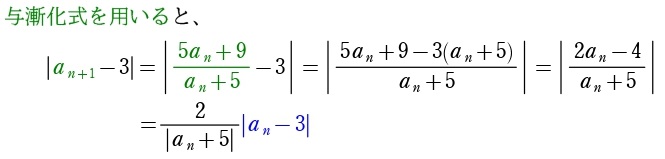



\(\displaystyle\frac{2}{|a_n+5|}\) を評価して \(●\)(ただし、\(0<●<1\))とします。今回は \(a_n>0\) なのでカンタン!
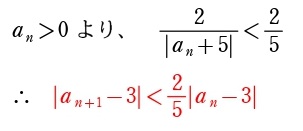
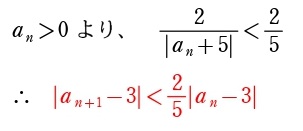
漸化不等式を繰り返し使う



目的は、
\(|a_n-3|<▲\) かつ \(\displaystyle\lim_{n\to\infty}▲=0\)
ですが、漸化不等式を↓のように繰り返し使うことで作れます。





結局結果は等比数列の漸化式を解くときと変わらないんですが、↑の過程は軽く残すのが慣例とされています。っつ~かもう \(\displaystyle\lim_{n\to\infty}4\left(\displaystyle\frac{2}{5}\right)^{n-1}=0\) で「はさみうちの原理」から \(\displaystyle\lim_{n\to\infty}a_n=3\) は当たり前なんで…
解答(完成版)



この残し方も含めて、完成版の解答↓を提示します。「ここまでの解答」では目的や漸化不等式も記述しましたが、採点者からすれば当たり前なので↓が書ければオッケーです!
.jpg)
.jpg)
誘導アリで解いてみよう!



ここまでの内容がおさえられていれば、誘導アリの冒頭の問題も怖くありません!解いてみよう!!
問題(2021信州大)


考え方
(2)で漸化不等式の導出が要求されていることに注目しましょう。漸化不等式の形から、\(\displaystyle\lim_{n\to\infty}a_n=3\) であることが分かるので、漸化式の両辺の \(n\) を \(\infty\) に飛ばして極限値を求める必要はありません。
(1)は、漸化不等式の公比っぽいもの
\(●\) の評価に利用する \(a_n\) の範囲の立式誘導
↓
数学的帰納法で証明
するのが常套です。暗記しておきましょう。
(2)の漸化不等式の立式ですが、漸化不等式の左辺に漸化式を代入した後、
漸化式がルート型 → 分子の有理化
を行うのが有名で…これも暗記して欲しい…



「暗記」・「暗記」と言い続けてしまって申し訳ないm(_ _)m
公比っぽいもの \(●\) の評価では、前述の通り(1)を用いますが、同値変形で導けば良いでしょう。
- 右左辺のどちらを採用するのか
- ルートを、問題文で登場する \(\displaystyle\frac{4}{5}\) が登場するように評価する
点に注意してください。
(3)は、(2)の漸化不等式を繰り返し用いて、はさみうちの原理を利用するだけです。



(1)・(2)が解けなかった人も、(3)は解くようにしてください。部分点はもらえます。
解答




応用型
漸化不等式の立式に「平均値の定理」を利用するタイプの問題も、非常に有名で上位校で頻出で、↓の記事で詳しく解説しております。


- 「平均値の定理」がビミョーな人は、↑の記事を最初から
- 「平均値の定理」が完璧な人は↑の記事のここのみ
ご覧くださいm(_ _)m
まとめ
こんな長い記事をここまでマジメに読んでくれたのに…



君の受験校で出題されなかったら申し訳ないm(_ _)m
でも、あまりに有名問題であるがゆえ、
上位校では、サービス問題として出題される
↓
全く手が出なかったら、そのテストは終わり
になっちゃいます。



恥ずかしながら…
現役で早稲田理工の僕…
現役時この問題ダメでした…
出題されなくて良かったぁ~
って恥ずかしい大人にならないように、頑張って解法を暗記してください!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!







