2026上智経済【数学共テ併用】解答速報
2025上智大学経済学部の共通テスト併用方式の数学の解答速報をお届けします！
めぐろ塾の安田人員不足のため、一人で孤独にやっております(笑)
ミスを見つけた方は、X（Twitter）のDM等でご指摘頂けますと幸いですm(_ _)m
また、問題を送ってくださった受験生の方に、厚く御礼申し上げますm(_ _)m
１
問題
考え方
めぐろ塾の安田初っ端からイヤなの来ましたね…
理系であれば、恒等式、
\[\left(\displaystyle\frac{\sqrt{3}}{2}x+\displaystyle\frac{1}{2}\right)^n=(x^2+1)P(x)+a_nx+b_n\]
を立式して、\(x=i\) を代入すれば、極形式で瞬殺できる問題なんですが…
文系だと、
(1)で、\(R_3(x)=-1\) となることを誘導として…
↓
(2)では、二項定理
と考えなきゃいけない問題で、そこそこ高レベルです。
めぐろ塾の安田上手く考えられなかった人も、(2)は当てカンで埋めなきゃダメ！
ノリ的に \(±\displaystyle\frac{\sqrt{3}}{2}\:,\:±\displaystyle\frac{1}{2}\) になりそうなので、符号を当てカンして埋めましょう。
なお、打ち込むのがダルかったので、解答では(1)を式変形で解いていますが、フツーに整式の割り算を使って解いてりゃオッケーです。
解答
２
問題
考え方
(1)は内積の定義式から計算するだけ。(2)はベクトルの三角形の面積公式
めぐろ塾の安田じゃなくても、(1)から \(\sin\theta\) を出して \(\displaystyle\frac{1}{2}\left|\overrightarrow{\textrm{OA}}\right|\left|\overrightarrow{\textrm{OB}}\right|\sin\theta\) で計算してもオッケー。
鬼門は(3)…
解答に軽い図説を入れておきましたが、
四面体の３等辺の頂点から底面に下した垂線の足は…
↓
底面の三角形の外心となる
ってのが公式化されてないと解けない問題です…
これさえ知っていれば、外心の１次結合で平面 \(\alpha\) 上の点を求め、Ｐの軌跡はこれを通り、平面 \(\alpha\) の法線ベクトル \(\overrightarrow{d}\) に平行な直線。(4)はこの直線と \(xy\) 平面の交点を求めて、四面体の体積を計算するだけですが…
めぐろ塾の安田計算量は少なくありません。(3)以降よく分からなかった人も、\(\overrightarrow{\textrm{d}}\) は平面 \(\alpha\) の法線ベクトルって当てカンして当てて欲しいところ。
解答
３
問題
考え方
めぐろ塾の安田Ｐ \((a\:,\:b)=(2\cos\theta\:,\:2\sin\theta)\) ってすぐ分かっちゃうので、全体的にただの三角関数の最大・最小。めぐろ塾↓
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
の三角関数のフローチャート↓
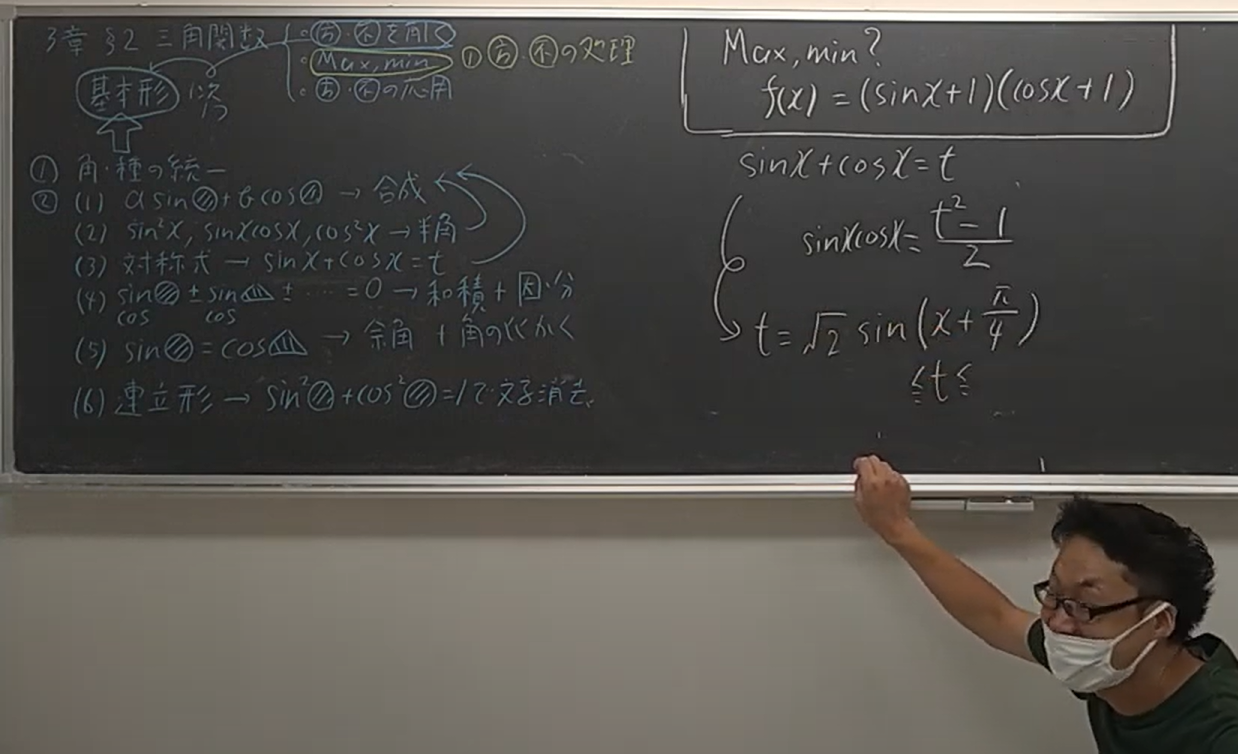
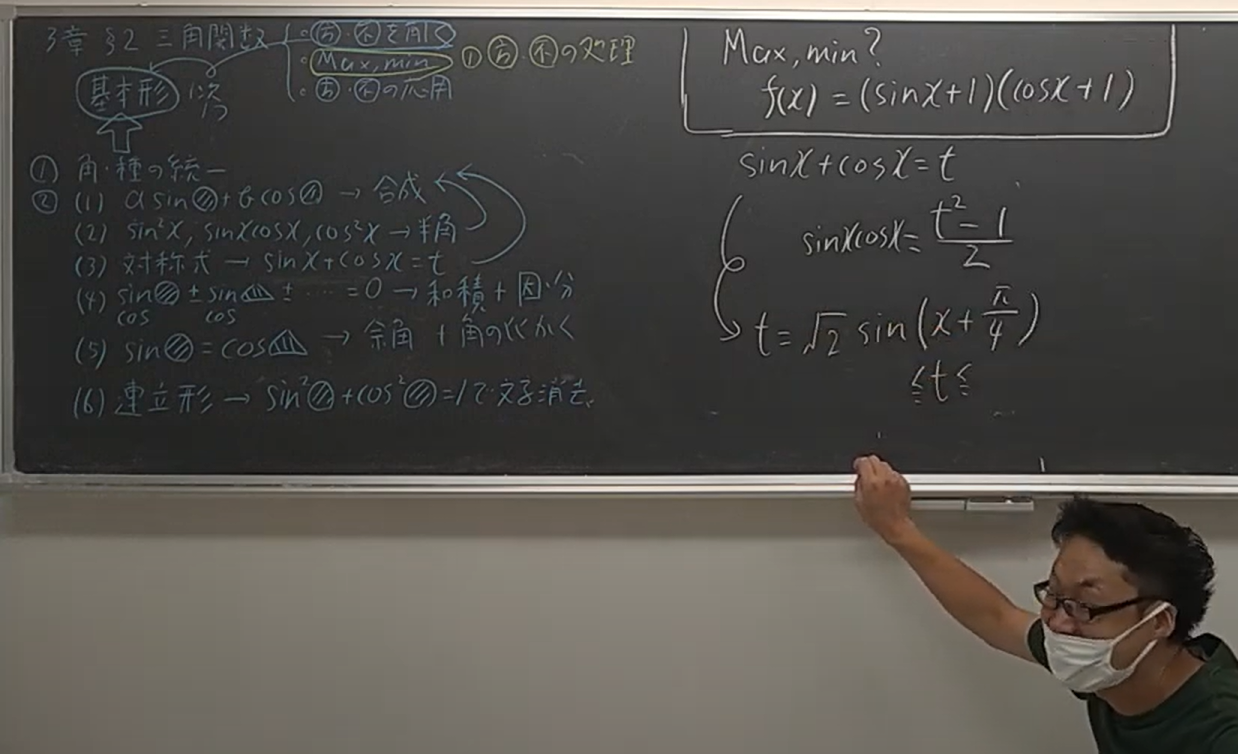
に従ってりゃ終了です。(1)は②（１）、(2)は②（３）、(3)は①。
(4)は \(\displaystyle\frac{b}{a}=1\) でカンタンすぎて怖くなっちゃいますが、tanの加法定理を使うだけ。
完答はマストな大問でしょう。
解答
４
問題
考え方
(1)は２つの放物線の共通接線立てるだけ。
＜解法１＞ \(\ell：y=mx+n\) を \(C_1\:,\:C_2\) と「連立して \(D=0\)」×２
＜解法２＞ \(C_1\) の接点をおいて接線を立式し、\(C_2\) と「連立して \(D=0\)」
＜解法３＞ \(C_1\) と \(C_2\) の接点をおいて接線を立式し、その一致
めぐろ塾の安田のどれでやってもいいです。解答では未知数の少なさから＜解法２＞でやりましたが、(2)で \(C_2\) の接点も必要になるので、＜解法３＞でやるのがベストかも。
(2)は典型的な接線との面積。解答では、
∫(上－下)dx → 因数分解 → 積分計算
という記述式でのルールを守りましたが、慣れている人であればほぼほぼ暗算できるでしょう。
(3)は、(1)を誘導とし、\(\ell\) の傾きを境目に場合分けして考えるだけ。
最後の大問ですが、思考的には一番平坦な問題でしょう。
解答
講評
去年2025の解答速報↓
も行いましたが、これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| マーク式、 一部答のみ解答 | 75分 | ４問 | やや難化 |
に思えます。
- 大問数が３問→４問に増えた
- 最初の１・２が解きづらい、イヤらしい構成
めぐろ塾の安田ってことで、ビビっちゃった人が多いでしょう。
１(1)・2の(2)まで・３・４を８割程度の精度で解ければ、合格最低点は固いテスト！
プラス２とかを完答できた人はかなり数学で稼げたんじゃないでしょうか？
めぐろ塾の安田でももう上智のことは忘れておっけ～。
早慶を併願している人が多いと思います。
切り替えて早慶に向けて頑張れっ！
君の受験はまだまだこれからだっ！！
めぐろ塾の安田そして僕の解答速報地獄もまだまだこれから…
大丈夫、君は一人じゃない(笑)
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
