2023早稲田人科【数学選抜】解説・解答・講評
2023早稲田大学人間科学部の数学選抜の数学の解説・解答・講評をお届けします！
めぐろ塾の安田人員不足のため、一人で孤独にやっております(笑)
確認役がいない、かつ東進過去問データベースにも解答が掲載されていないため、最終的な値には全く自信がありません(笑)ミスを見つけた方は、TwitterのDM等でご指摘頂けますと幸いですm(_ _)m
【問１】（必須問題）
問題
考え方
例年通り、小問集合３題です。
(1)は…
めぐろ塾の安田ＡとＢのカードの組み合わせを愚直に数えるしかない気がします…
少なくとも私めは効率的な計算は思い浮かびませんでした(笑)
計算が煩雑です。記述式なので、途中過程を詳細に記述し、部分点を狙いに行った方が良いでしょう。そして、計算が煩雑なため、最終結果には全く自信がありません(笑)数学強者の皆様、間違えを見つけたらご指摘お願いしますm(_ _)m
(2)は、円と放物線の囲む面積計算なので、完答はマストでしょう。放物線の方の面積計算は１／６公式を使っても使わなくてもどっちでもいいです。解答では、対称性に注目し、使わない方向で計算しています。
(3)は、めぐろ塾のフローチャート↓通り。②の（２）です。
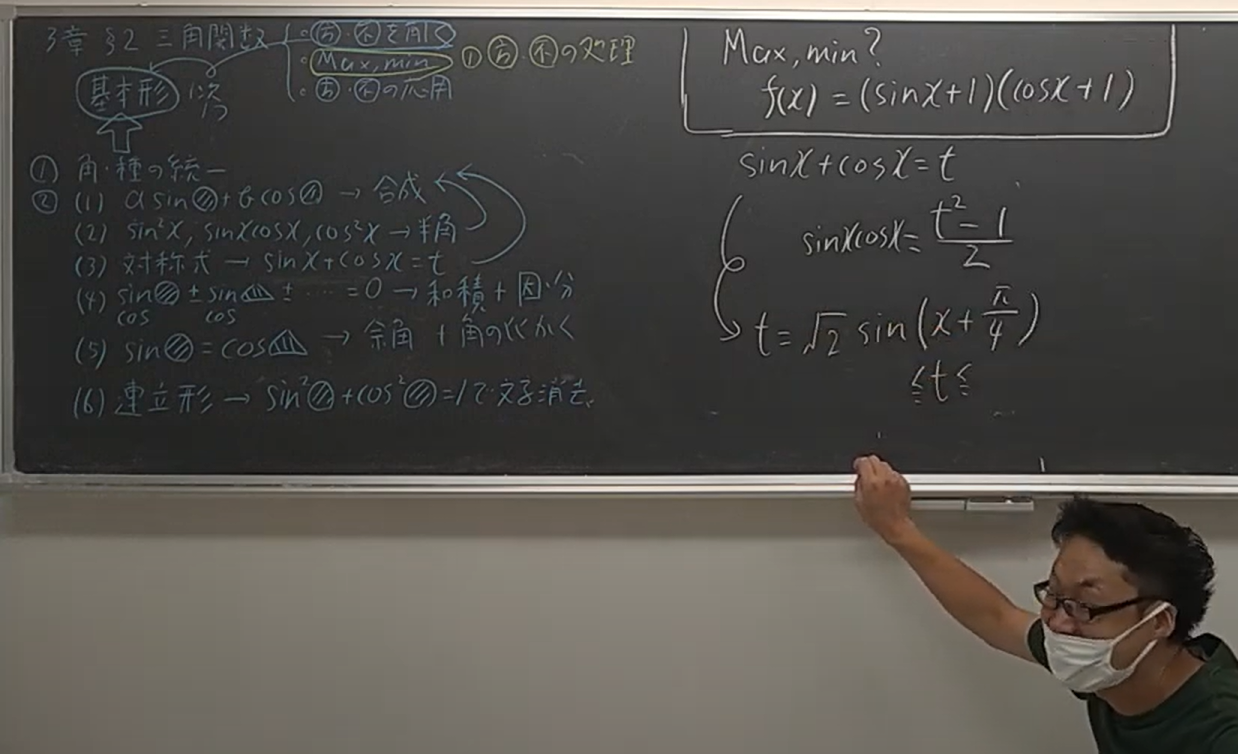
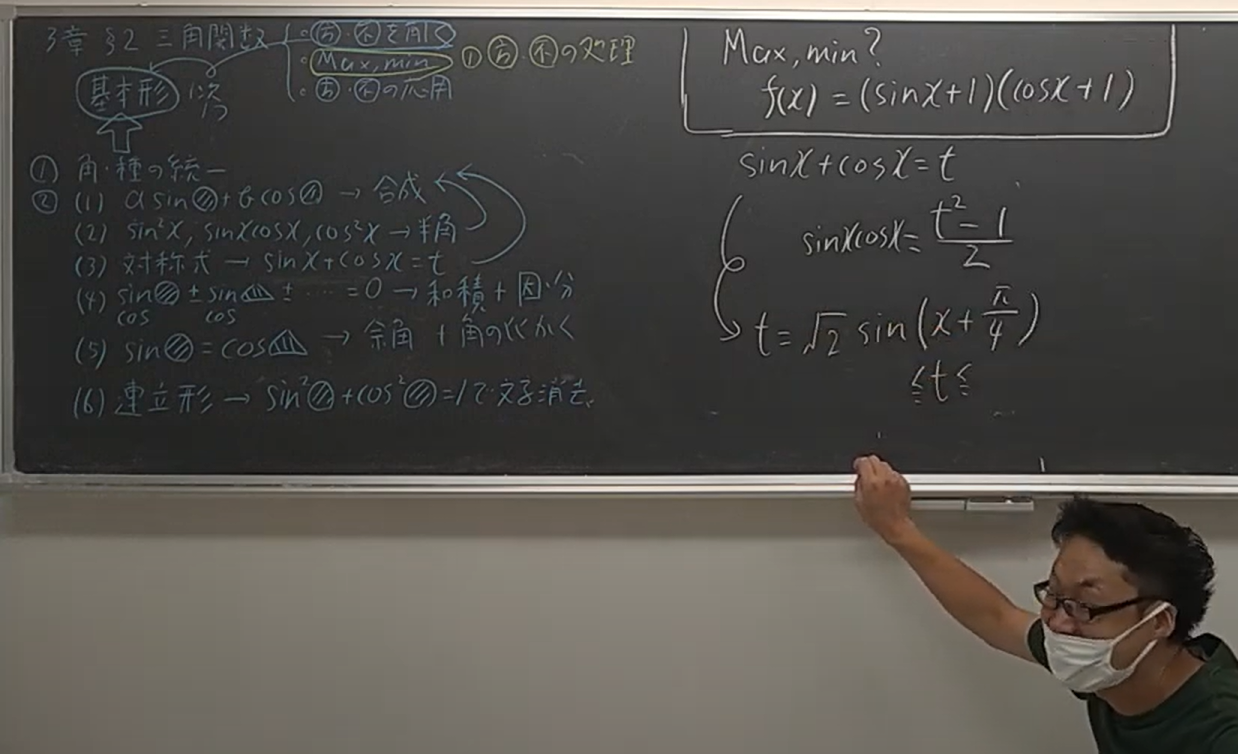
流石に早稲田なんで合成角が分からないタイプになりますが、冷静に計算しましょう。この言葉の意味が分からない人は、めぐろ塾↓へのご入塾をご検討ください(笑)
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
解答
【問２】（必須問題）
問題
考え方
この問題は受験者の出来は良くないでしょう。
めぐろ塾の安田皆が大っ嫌いな「ガウス記号」の問題です。
安心して、プロ講師の僕も大っ嫌い(笑)
でも(1)は絶対に当てましょう。ガウス記号は整数に決まっているので、\(y\) を消去、\(x\) を消去して、\(3x\) と \(3y\) をガウス記号の和・差・積で表せば証明終了です。
(2)は僕も戸惑いました。恐らく解答のように、
カンタンな方の下式に \(x-1<[x]≦x\:,\:y-1<[y]≦y\) を利用
（ガウスを幅１で挟む）
↓
\(y\) を消せるので、整数 \(3x\) の範囲を絞り込み
↓
\(3y\) が整数となるものを答とする（十分性の確認）
がベスト解答だと思うんですが、これに至るまでに悩むこと10分(笑)
ガウス記号とはさみうちの原理の融合問題に慣れている理系の人が有利な問題に感じます。文系の人は(2)は解けなくていいんで、他の問題で挽回しましょう。
解答
【問３】（必須問題）
問題
考え方
例年通り、やはり再び小問集合です。
(1)は…
めぐろ塾の安田カンタンに見えてムズそ～
と思ったらクソ簡単でした(笑) \(2^3=8>7\) と \(2^4=16<17\) を使うだけ。
(2)はムズいです。2023一橋大４とかの問題に慣れていないと、まず「群数列」の問題であることに気づけないでしょう。そして、気づけたとしても処理は楽ではありません。
めぐろ塾の安田2023一橋大４の並べ方は典型なんですが、今回の並べ方は僕も初見で、戸惑いました。
混乱せずに解くためには、
１を第０群と設定
↓
第 \(n\) 群の四隅が \(±n\) 行 \(±n\) 列となるようにする
必要があります。これで僕の解答ミスってたら本望なんですけど、ミスってたらご指摘お願いしますm(_ _)m
(1)は絶対当てて欲しいですが、(2)は外しちゃってもしょうがないと思います。因みに作問的に(2)はほぼ答のみで採点してると思うんで、あまり論証とかを詳細に記述するよりも、解き方が分かったら答を当てにいった方が良いでしょう。
解答
【問４】（選択問題）
問題
考え方
文系生徒用の選択問題です。数Ⅲ範囲の知識がいらない選択問題となっています。
(1)は、またしてもめぐろ塾のフローチャート↓通り。②の（３）です。
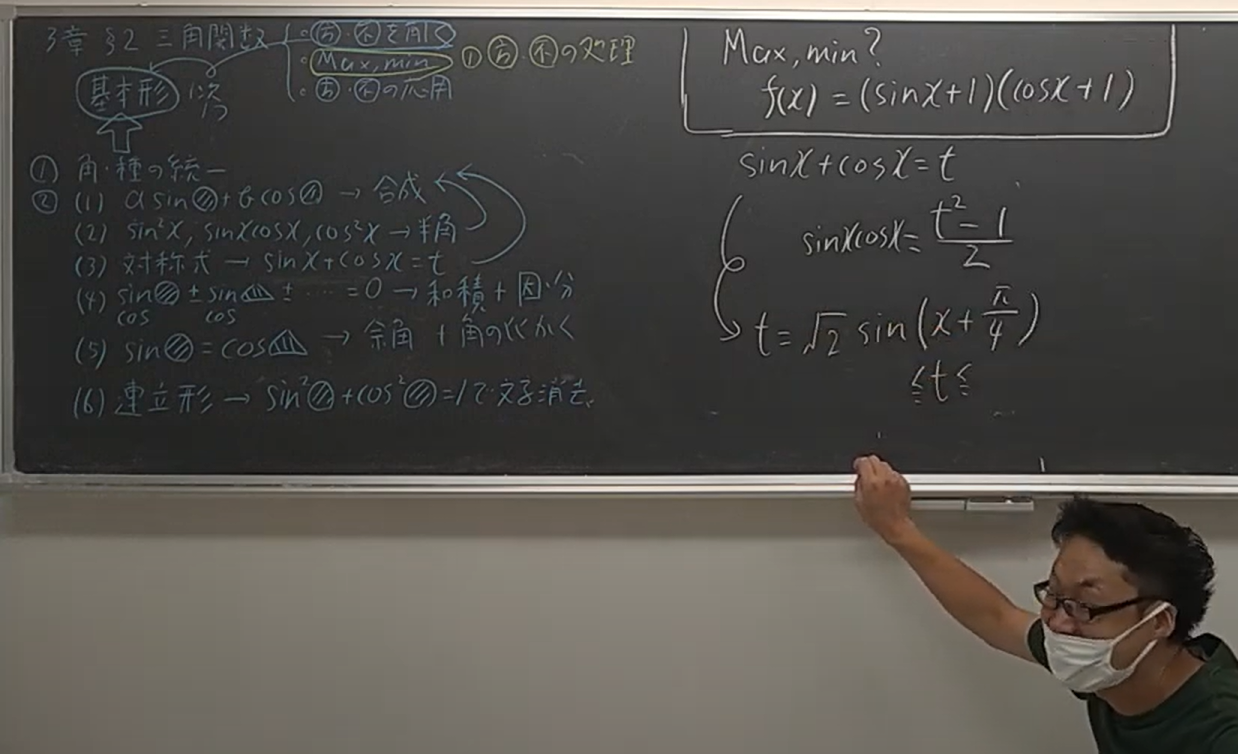
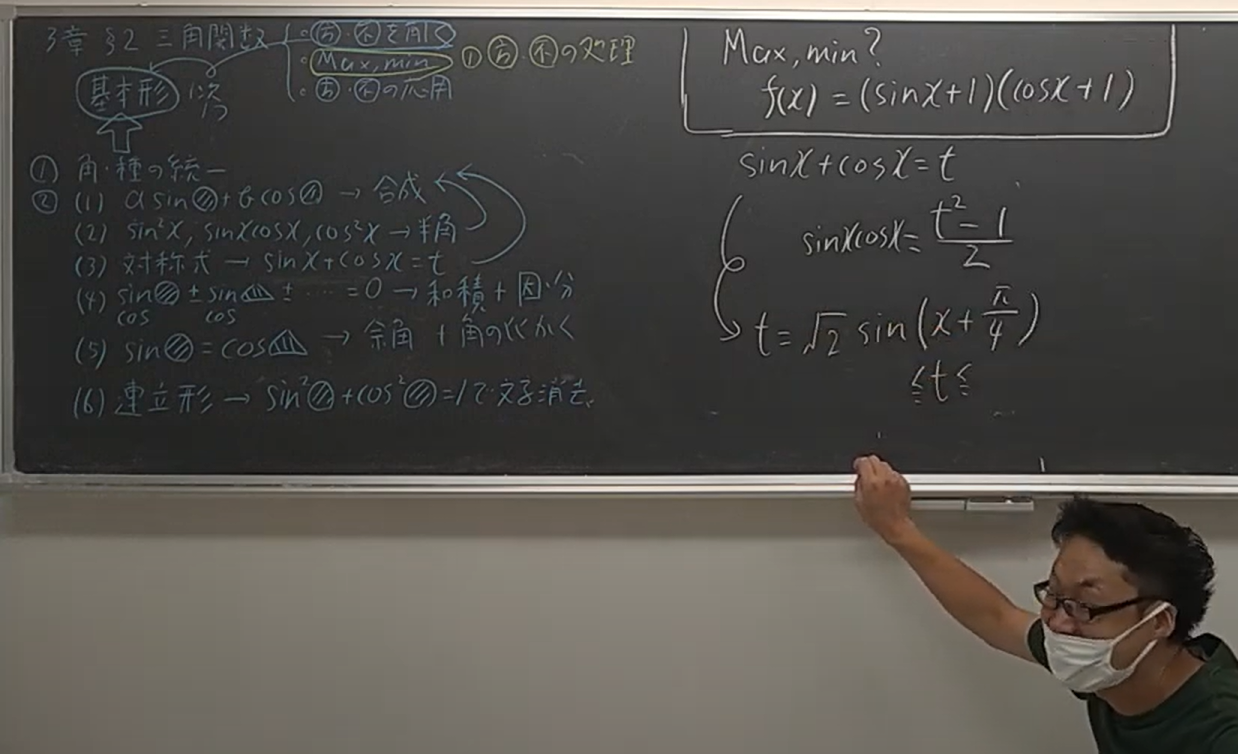
ってかこの授業でやってる問題（画像右）と全く同じ形ですね(笑)めぐろ塾だと、
三角関数の対称式は、\(\sin x+\cos x=t\) とおく
↓
\(\sin x\cos x=\displaystyle\frac{t^2-1}{2}\) となる
ってとこまで暗記させます、あまりにも頻出なので。流石に早稲田なんで、これは当たり前とし、
解の個数が問われている問題で、\(x\) の式を \(t\) でおいた
↓
\(t\) と \(x\) の個数対応を調べないとアウト
って作問になっております。でもこれも、めぐろ塾では「個数対応チェック」って形で定型化させるくらいの典型作業なので、本校受験者であれば(1)の完答はマストに思えます。
そして(2)の(a)の完答もマストです。ただ不等式を解き、その範囲内の整数 \(x\) を解答するだけ。
めぐろ塾の安田でも…(b)は結構厳しいっす…
解答では、
最初の与不等式の形から、\(x=-1\) は絶対に解となることを見抜く
↓
\(-1\) を含む連続３整数が解となるように \(x\) 軸相手に放物線のグラフを考える
（３つで場合分け）
としましたが…メンドくさいです…
もっと上手い解法がないか探しましたが、\(a\) が整数じゃないのでこれしかないような気がします。因みに計算が煩雑なので、最終結果にはやはり全く自信がありません(笑)ミスを見つけた方はご指摘お願いしますm(_ _)m
解答
【問５】（選択問題）
問題
考え方
理系専用範囲の数Ⅲからの出題です。
めぐろ塾の安田理系生徒は絶対に【問４】よりこっちを選択した方が良い。
クソ簡単。
(1)は、ただの合成関数の微分（外微分×中微分）。
(2)は、(1)の結果を利用して接線公式、原点の通過条件を処理するだけ。
(3)は、(2)の結果を利用してネイピア数 \(e\) の定義式から極限計算するだけ。
計算量も少なく、最後の問題にして超サービス問題です。
解答
講評
2022の解説記事↓
も作成しましたが、これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 120分 | ５問 （【問４・５】は、どちらかを選択して解答。文系は【問４】を選択するしかない） | 変化なし |
に思えます。
- 選択問題の難易度が、文系生徒用の【問４】＜＜理系生徒用の【問５】
- 【問２】(2)はガウス記号に慣れている理系生徒でないと厳しい
といったことから、
理系生徒がかなり有利な構成
となってしまいました。
めぐろ塾の安田ま～でも公表されている合格最低点は６割を切っています。数学力のある文系の人であれば、これはクリアできるでしょう。
【問１】(2)・(3) ＋ 【問２】(1) ＋ 【問３】(1) ＋ 【問４】(1)・(2)(a) の完答で、６割弱にはなる！
ので。
めぐろ塾の安田理系の人であれば、「【問４】(1)・(2)(a)」の部分を「【問５】完答」とできるので、６割には非常に乗せやすいテストです。
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
