2023慶應商【数学】解答速報

2023慶應義塾大学商学部の数学の解答速報をお届けします!
 めぐろ塾の安田
めぐろ塾の安田ま~もう「速報」とは言えず「遅報」なんですけどね(笑)
今後の記事で使う可能性が高いんで、私めの解答はここにさらさせて頂きますm(_ _)m
Ⅰ
問題
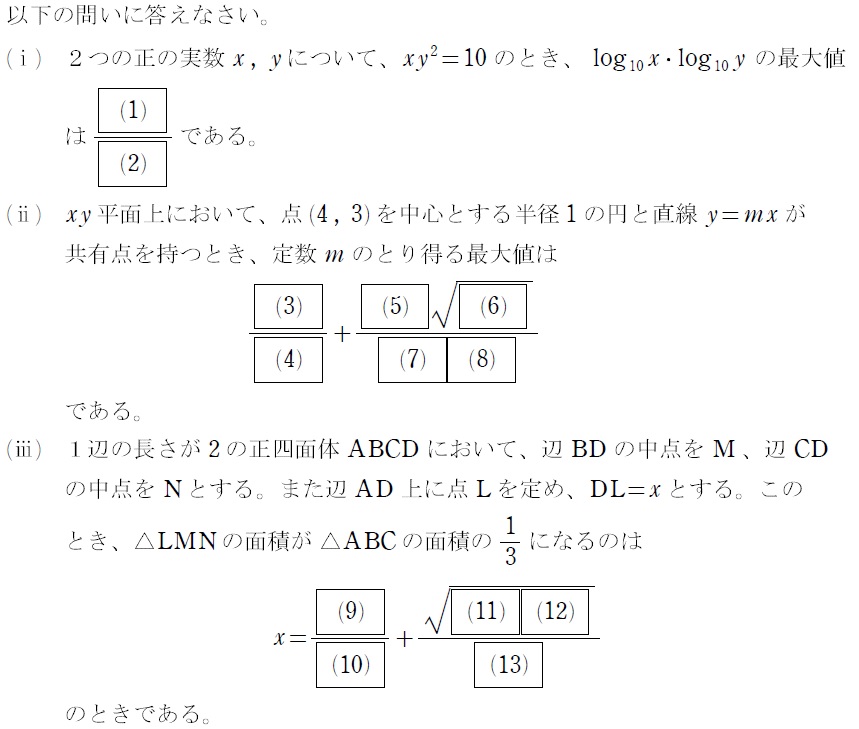

考え方
(ⅰ)は、\(\log\) の積の形があるので置き換えです。\(\log_{10}x=X\:,\:\log_{10}y=Y\) とおき、\(xy^2=10\) の両辺の常用対数をとった式から文字消去を行って、2次関数の最大に持ち込みましょう。



因みに置き換えしたときは変域を調べるのが普通だけど、全実数になるから解答ではそこは省きました。最大値をとる変数の値の明記も省いた、ど~せマーク式だし(笑)
(ⅱ)は、「円と直線が共有点を持つ」→「\(d≦r\)」ってのが公式化されてれば瞬殺。
(ⅲ)は、
- 「立体は断面を抜き出して考える」ってゆー基本を守る
- 「正三角形」=「二等辺三角形」と中点がたくさん登場してるから、「二等辺三角形を見たら即座に半分に割る」を使いまくる
だけですが、受験者の出来は良くない気がします。



文系だと空間に拒絶反応おこす人多いよね(笑)
解答の断面AEDのAから下ろした垂線の足は底面の重心になります。正四面体の体積計算で使う断面だから、この経験ある人が有利かな
解答


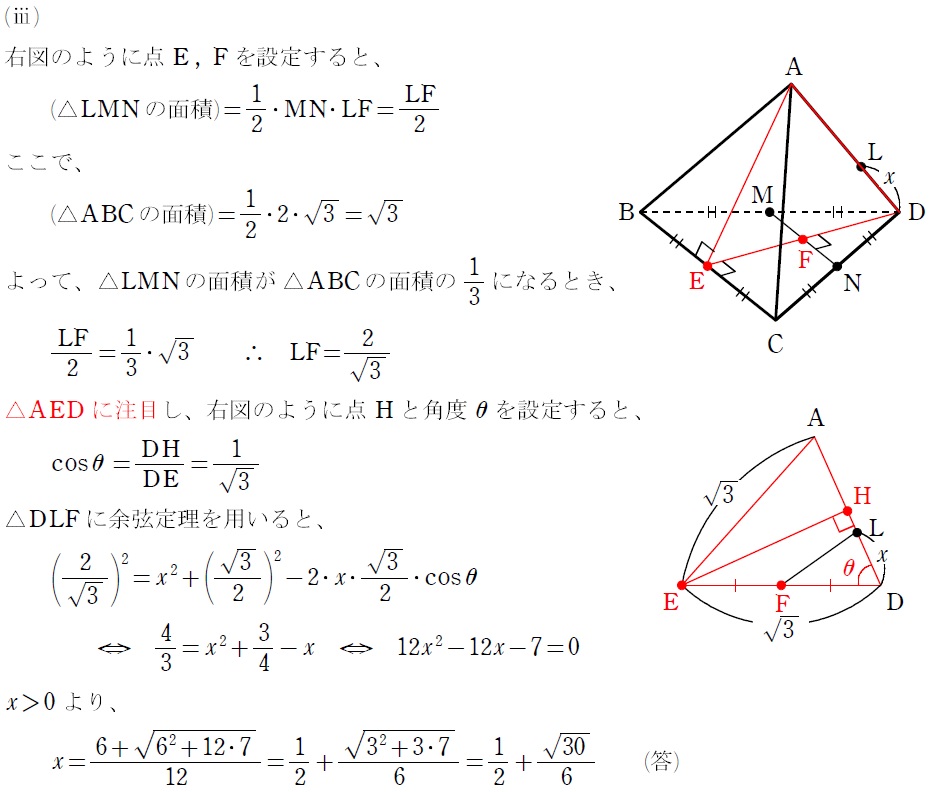

Ⅱ
問題
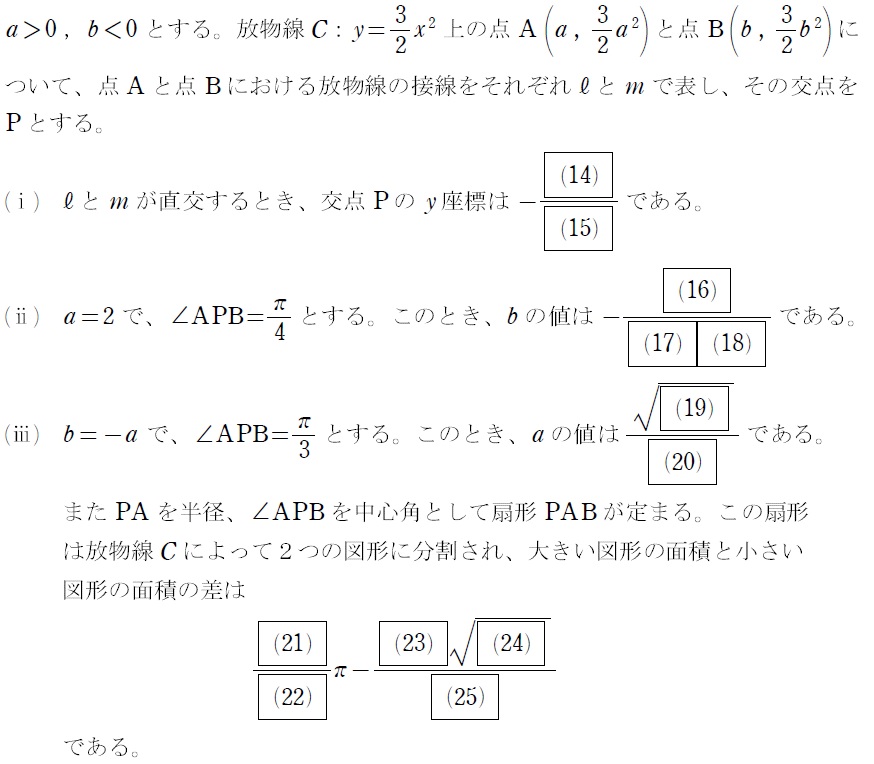



- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
考え方
文系での求積の出題の3割くらいを占める、「放物線と2接線の囲む面積」についての問題です。なんで良くでるかってゆーと、どんな放物線に対しても…
- 2接線の交点の \(x\) 座標は、接点の \(x\) 座標の平均
- 「2接点と放物線の囲む面積」:「2接線と放物線の囲む面積」=2:1
になるから。



記述式では証明なしで使っちゃダメだよ!
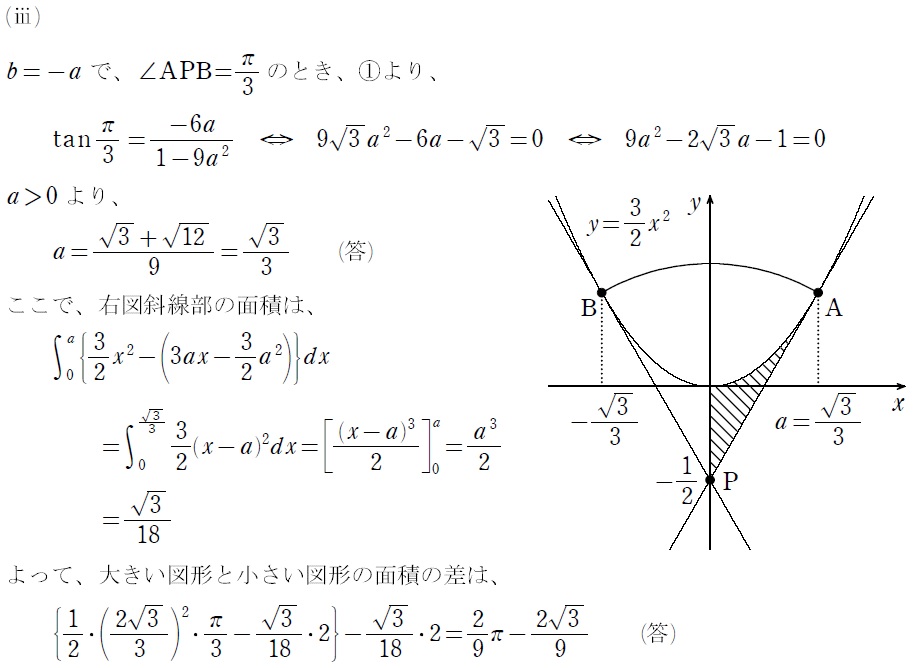
今回はマーク式ですが、知ってても(ⅰ)、(ⅲ)の後半がちょっと簡単になるくらい。一応解答では、(ⅲ)の後半の面積計算で上は使わず、∫(上-下)dx=∫(因数分解)dxで代入箇所を減らして計算する、ってゆー記述式での模範解答を載せておきます。
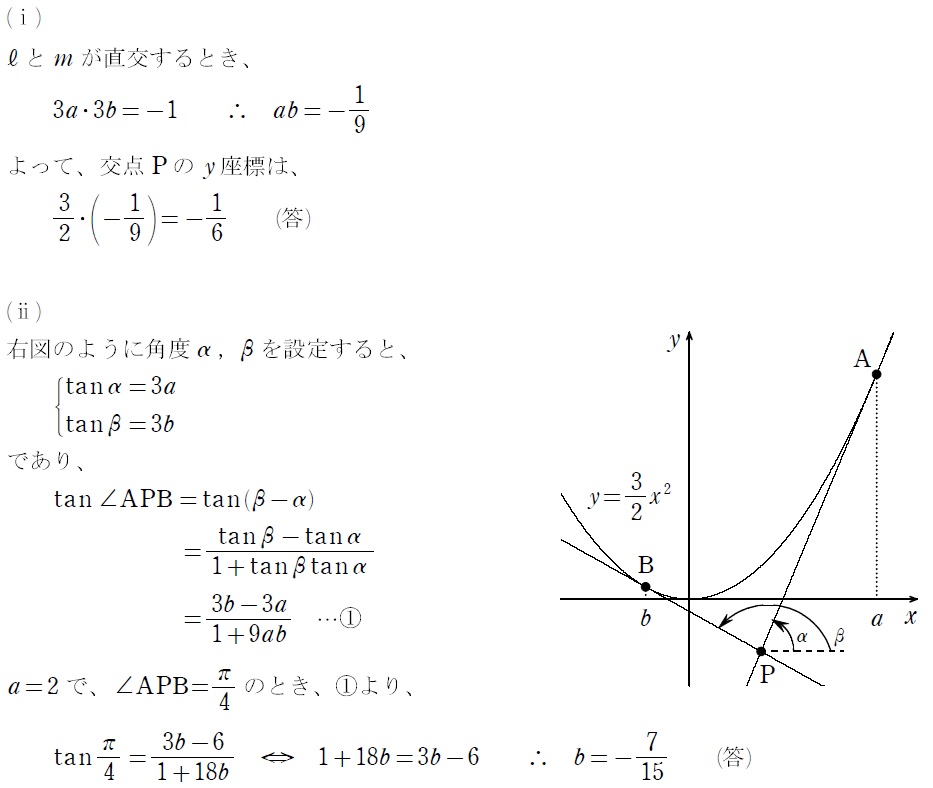
他は「座標平面上での2直線のなす角」→「\(\tan\) の加法定理を利用」ってゆー有名処理です。
解答
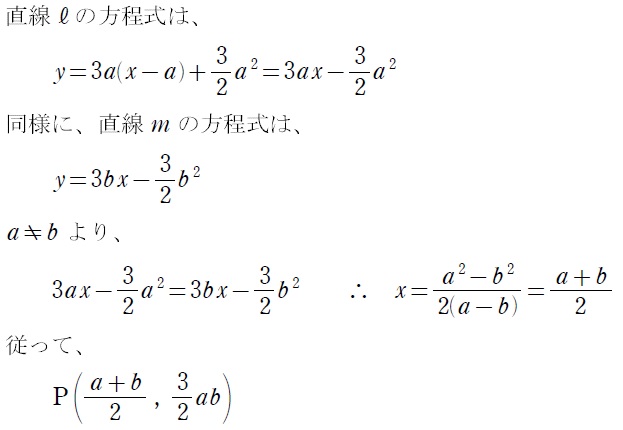
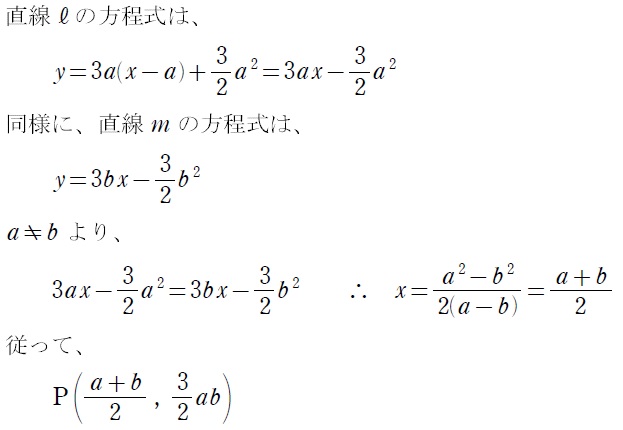


Ⅲ
問題


考え方
(ⅰ)は、この記事のここで紹介してる「1次結合」の<解法3>を用いるだけです。



(ⅱ)が鬼門ですね。同じことの繰り返しだから…
漸化式を立式するのは明白なんですが、フツーに考えると3項間漸化式になるので、
ベクトルで3項間漸化式なんて使っていいの?



って思う人が多いかと。安心して、解いてて僕もそう思った(笑)
発生する演算が和・差や実数倍だけなので、通常の3項間漸化式と同様に処理できます。ま~でも初項の考察もムズイので、受験者の出来は良くないでしょう。
因みに、他の解答速報さんで \(\overrightarrow{\textrm{P}_{n+1}\textrm{P}_{n+2}}=-\displaystyle\frac{1}{5}\overrightarrow{\textrm{P}_{n}\textrm{P}_{n+1}}\) を立式して2項間漸化式で処理する解答を載せてるとこがあって、個人的に感動しましたが(笑)計算量的なメリットはありません。
(ⅱ)さえできれば、(ⅰ)と(ⅱ)の結果を使った計算ってだけで、(ⅲ)は簡単です。
解答




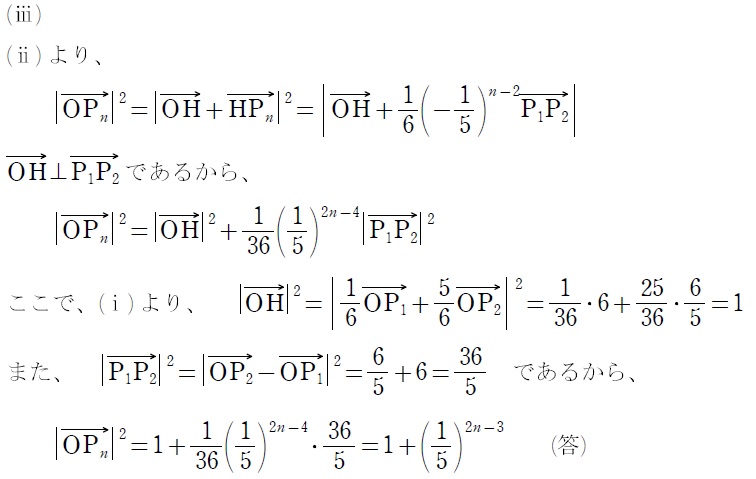
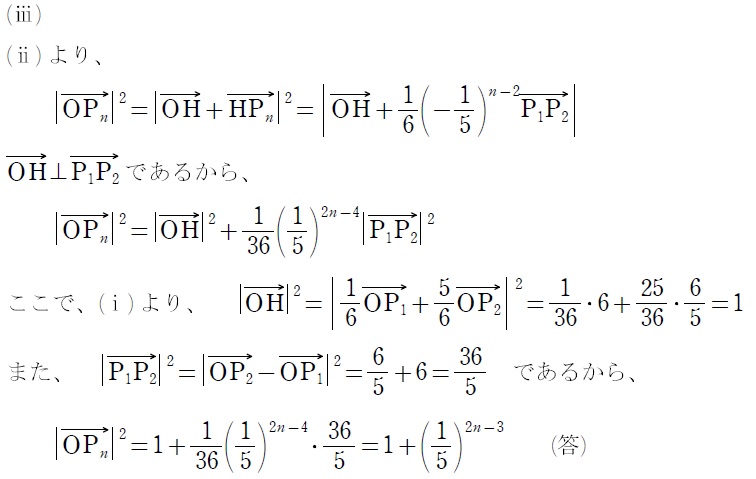
Ⅳ
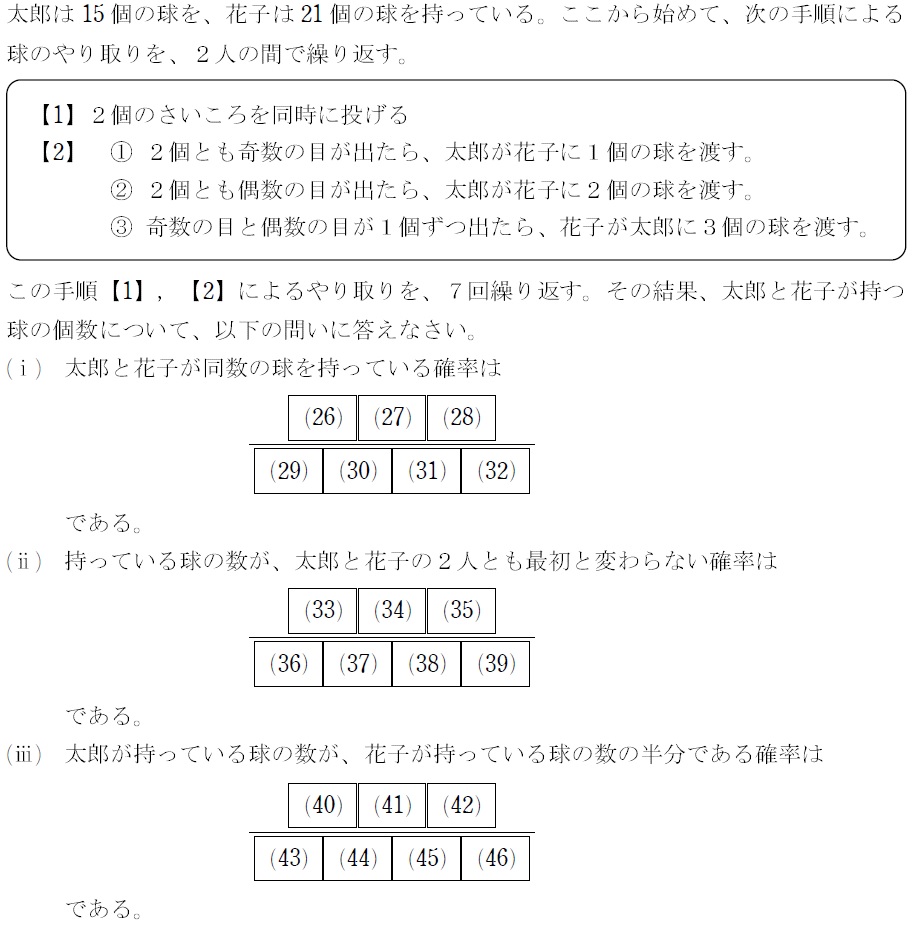
問題

考え方
全体を通じて、7回中①~③が何回ずつ起きるかを把握し、独立試行の定理で計算するだけの問題です。



(ⅰ)、(ⅱ)は場合分け発生せず、(ⅲ)も場合分け2つ!
って聞くと簡単に思えると思いますが…①~③が起こる回数についての不定方程式を立式しないと、かなりキケンな問題です。太郎の持ち球の個数が増えると、花子のが減るんで。解答では、太郎の持ち球の個数に注目して不定方程式を立式しています。
因みに(ⅰ)~(ⅲ)の各設問で立式できる不定方程式は、\(a\:,\:b\) を評価して \(c\) の範囲を絞ることで厳密に整数解を求めることもできますが…



係数の大きい \(c\) を0から固定していって整数解を見つけちゃえばいいと思います、マーク式だし(笑)
解答




講評



2022は問題流し見してムズそうな問題だけ解いただけなんですがm(_ _)m大手さんの解答速報を見ても…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| マーク式、 一部答のみ解答 | 70分 | 4問 | 変化なし |
だと思います。
商業的題材の長文問題が出題されることがある!
2018・2017・2015・2012で大問一題ずつ、2008・2007に至っては大問二題も!2022のⅣもちょっとこれに近いです。
この出題がない分、解きやすい年と言えるでしょう。



それでも…計算量も多いし…試験時間も短いし…十分キツイですけどね(笑)
試験時間的に、全ての問題を完璧に解くのは厳しいでしょう。難易度的にはⅢが一番ムズイので、
「Ⅲの(ⅱ)以降は外しちゃって約80点」から8割を獲得=約65点 で例年の合格最低点に持っていく!
のがベストに思えます。



Ⅰ・Ⅱ・Ⅳで失点をどれだけ減らせるかが勝負!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








