「ユークリッドの互除法」を徹底解説！
めぐろ塾の安田高校生のころ「ユークリッドの互除法」が大っ嫌いだったプロ講師の私めが…
「ユークリッドの互除法」を徹底的に分かりやすく説明して差し上げますm(_ _)m
結論：余りとの最大公約数にしていいよ
めぐろ塾の安田ってだけです。
でも…
ただ丸暗記しようとしても覚えられないと思うから…
感覚的に理解しましょう！
5267と5221の最大公約数を考えてみよう！
結論から言うと、それぞれの素因数分解は、
\[5267=23×229\:\:,\:\:5221=23×231\]
なので、最大公約数は \(23\) です。でも…
めぐろ塾の安田この素因数分解にどれくらい時間かかんねん！！！
って問題が発生(笑)
小さい方の \(5221\) を素因数分解するのに、
- \(2\) を素因数に持つか → 一の位が偶数でないから持たない
- \(3\) を素因数に持つか → 各位の数字の和が \(3\) の倍数でないから持たない
- \(5\) を素因数に持つか → 一の位が \(0\) または \(5\) でないから持たない
- \(7\:,\:11\:,\:13\:,\:17\:,\:19\) を素因数に持つか → 実際に \(5221\) を割って試しましょう！割り切れません！
- \(23\) を素因数に持つか → 実際に \(5221\) を割ると割り切れます！おめでとう！！
とゆ～とてつもない手間が…
そこで…
ことに注目してみましょう。
\[5267-5221=46\]
なので、\(46\) も最大公約数の倍数です。\(46\) の素因数分解は、
\[46=2×23\]
であり、２数 \(5267\) と \(5221\) は奇数なので、この時点で最大公約数は \(1\:,\:23\) のどちらかであることが分かってしまいます。
めぐろ塾の安田後は実際に \(5267\) と \(5221\) が \(23\) で割り切れるかを試すだけ。
まずは、差に注目することで、手間が大幅に削減できることを意識してください！
3239と1027の最大公約数ならどうする？
これらの最大公約数を「〇」としてイメージしてください。さっきのように差に注目しようとしても…
ことになります。
めぐろ塾の安田でも諦めずに…
もう１回引いてみよう！
めぐろ塾の安田さっきより短くなりました！
でもまだ1027より大きい＝長いので…
もっと引いてみましょう！
ことが分かります。さて、この残った部分は何かと言うと…
3239を1027で割った余り
です。余り \(3239-3×1027=3239-3081=158\) は元の２数 \(3239\) と \(1027\) より小さいので、確実に状況はカンタンになります。
\[158=2×79\]
で２数 \(3239\) と \(1027\) は奇数であることから、\(79\) で割り切れるかを試すだけ。
\[3239÷7=41\:\:,\:\:1027÷79=13\]
で割り切れるので、最大公約数〇\(=79\) であることがカンタンに分かります。
一般化すると…
めぐろ塾の安田「ユークリッドの互除法」への嫌悪感が消えるまでは(笑)
前項のイメージから常に導いた方がいいです。
２つの自然数 \(a\:,\:b\)（\(a>b\)）について、
めぐろ塾の安田ことを意識して…
ユークリッドの互除法
２つの自然数 \(a\:,\:b\)（\(a>b\)）について、\(a\) を \(b\) で割った余りを \(r\) とすると、
「\(a\) と \(b\) の最大公約数」＝「\(b\) と \(r\) の最大公約数」
余りとの最大公約数にしていいよ
が成立し、これを繰り返し用いると、２数が大きい場合の最大公約数を効率的に計算できる。この方法を「ユークリッドの互除法」と言う。
１問練習してみよう
めぐろ塾の安田取りあえず余りとの最大公約数にするとカンタンになるってのを強調してきたので…
前項の「繰り返し」って部分を補完します。
これまでの２例では余りがそこそこ小さい数字になったので、余りを素因数分解して最大公約数を求めましたが、実際の受験の出題では余りも大きい数字になることがほとんどです。なので、
「余りとの最大公約数にしていい」ってのを割り算しまくって繰り返す
ことになります、倍数・約数関係が出るまで。取りあえず、次の＜例題１＞で練習してみましょう。
＜例題１＞
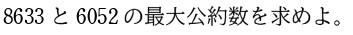
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
教科書の解答
めぐろ塾の安田教科書では、機械的に割り算を繰り返す解答が掲載されています。個人的にはこれキライなんですよね(笑)
めぐろ塾オススメの解答
めぐろ塾の安田余りとの最大公約数にしていいってことから、その都度言葉にした方がいいです。ってか必ずしも小さい方の数字を使う必要はないので、最後は \(801\) じゃなく \(890\) を使った方がカンタン。
厳密な証明
めぐろ塾の安田正直、ユークリッドの互除法の厳密な証明は、知らなくても大学受験ではほぼほぼ困りません！
でも、一応2005の広島市立大で出題されているので載せておきます↓
問題
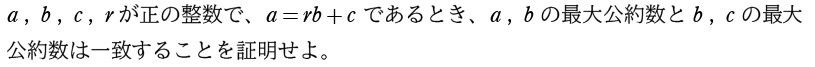
考え方
\(a=rb+c\) → \(c\) は、\(a\) を \(b\) で割った余り
めぐろ塾の安田のようなもの
です、\(c<b\) が言われていないので。厳密には「何回か引いた残り」ですが、あまり気にする必要はありません。
\(a\:,\:b\) の最大公約数と \(b\:,\:\)\(c\) の最大公約数は一致
↓
余り \(c\) との最大公約数にしていい
ことの証明なので、「ユークリッドの互除法」の証明と言えます。
「最大」公約数の一致を言おうとすると、「互いに素」とかを言及しなきゃいけなくてダルい
↓
解答のように、公約数の「集合」としての一致を証明するのがカンタン
です。
解答
使用ケース
「ユークリッドの互除法」の大学受験における使用ケースは以下のようになります。
- 先に紹介したような、大きい２数の最大公約数を求めるとき
- 応用問題での活用（文字式の公約数等）
めぐろ塾の安田ここで…
おいおい…
「２変数１次不定方程式の整数解を求めるとき」に使うだろ！？
って思えた人は優秀なんですが…
２変数１次不定方程式では事実上いらない…
めぐろ塾の安田以降、下記の＜例題２＞の解き方は分かっているものとして解説を進めます。
＜例題２＞
解答
めぐろ塾の安田要点をまとめると…
１解を見つける
↓
それを代入した式との差をとって、定数項を消去
↓
同じ文字（解答では \(k\)）で表す
ってなるんですが…
＜例題３＞
めぐろ塾の安田係数が共に２ケタ以上になる場合は「１解を見つける」のが厳しくなるんですよね…
ここで、教科書では「ユークリッドの互除法」で係数 \(49\) と \(23\) の最大公約数 \(1\) を求める過程を遡って「１解を見つける」作業を行います。
教科書の解答
めぐろ塾の安田これ↑…
結構ムズくない？(笑)
僕、未だに↑のように「主役はこの２つ～」ってしないと混乱します。
他の予備校の解答速報とか打つときは、「コイツ教科書読んでね～のか～？」って監視役に思われないように僕も↑の解答を打ちますし…
誘導がついたときのために↑の解答も理解しておくのが理想ですが…
教えてても体感的に少なくとも10人中９人は…
こっちの方がカンタンじゃね？
めぐろ塾の安田って思うはず。
小さい方の係数でくくって、置き換え
＜例題３＞再掲
めぐろ塾オススメの解答
めぐろ塾の安田一部の教科書はこっちの方法を「発展」とか「参考」とかで載せてるんですけどね、こっちを本解答にして欲しい(笑)
めぐろ塾の解答速報では当然こっちを使っています。
因みに、見かけ上の答がさっきと違いますが、↑の \(k\) に \(k+1\) を当てはめるとさっきの答が出てくることになり、結局どっちも同じ整数解を表しています。
まとめ
徹底的に解説してきた通り、「ユークリッドの互除法」なんて…
めぐろ塾の安田余りとの最大公約数にしていいよ
って言葉でおさえておけば、大学受験では困りません。
めぐろ塾の安田現役時の僕のように捨てるのはやめましょう！
…本番で…
たまたま出題されなくて…
良かった(笑)
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！
- 日本全国どこからでも受講可能！
- 完全個別指導コースあり（オンラインも可）！
- 初回面談・初回授業は完全個別で無料（オンラインも可）！
めぐろ塾の安田初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります（セールス・勧誘のお電話は固くお断り致します）。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます！
