「安田の定理」を徹底解説!

大学受験数学界のレジェンド「安田亨」先生が発見した「安田の定理」を…
 めぐろ塾の安田
めぐろ塾の安田奇遇にも同じ苗字の私めが徹底解説させて頂きますm(_ _)m
「安田の定理」について
「安田の定理」とは、以下のようなものです。
安田の定理
分数関数 \(h(x)=\displaystyle\frac{g(x)}{f(x)}\) が \(x=\alpha\) で極値をとるとき、\(f'(\alpha)≠0\) ならば、その値は、
\[h(\alpha)=\displaystyle\frac{g'(\alpha)}{f'(\alpha)}\]
である。
微分すると多くの関数はカンタンになるので、極値をとる \(x\) の値が汚いときの極値計算を簡略化してくれる定理です。発見者の「安田亨」先生の名前に由来し、大学受験数学界では「安田の定理」と呼ばれています。



僕じゃないですよ(笑)
「安田亨」=「偉い安田先生」
「めぐろ塾の安田」=「偉くない安田先生」
そんな「偉くない安田」が「偉い安田先生」をディスるようになってしまって申し訳ないんですが…
覚えておく必要は全くない!
詳しくは後述しますが、大学受験数学で恩恵が得られるケースはほとんどありません。



偏差値60もないバカほど、こ~ゆ~マイナーテクニックを覚えて喜ぶんですけどね…
ここで言う偏差値とは「高3・高卒時の河合塾全統記述模試」のものです。この偏差値が一番信頼できるってことについては↓の記事をご覧くださいm(_ _)m


「偉い安田先生」=「安田亨」先生に代わって、「偉くない安田」が代弁しておきますが…



数学の偏差値65いってないなら、「安田の定理」を覚える資格はない!
です。よって、偏差値65いってない人はもうこの記事閉じちゃってください。
偏差値65以上の人が覚えようとするならば…
覚え方
分母・分子を微分したものに置き換えて良いということから、君らにとって常識の「ロピタルの定理」↓と類似しています。
ロピタルの定理
\(\displaystyle\lim_{x\to a}\displaystyle\frac{g(x)}{f(x)}\) が \(\displaystyle\frac{0}{0}\) または \(\displaystyle\frac{\infty}{\infty}\) の不定形となるとき(\(a\) は \(\infty\) でも良い)、
\[\displaystyle\displaystyle\lim_{x\to a}\displaystyle\frac{g(x)}{f(x)}=\displaystyle\lim_{x\to a}\displaystyle\frac{g'(x)}{f'(x)}\]
ただし、右辺の極限値が存在するときに限る。
これと併せて覚えれば良いでしょう。使用条件もこれと同様で…
記述式解答に「安田の定理」の使用痕跡を残しちゃダメ!
「ロピタルの定理」は証明が大学数学内容のため、検算テクニックとして君臨していることは、偏差値65を超えている君たちにとっては常識でしょう。教科書には記載されていない「安田の定理」の使い方も同様で、記述式解答に使用痕跡を残してはいけません。
証明



一応「安田の定理」の証明も載せておきます↓


「安田の定理」の使い方
使えるケース



と言った通り…使えるケース(使ってメリットのあるケース)が非常に限定的です。
- 分数関数の微分=0で、2次方程式の解の公式を使った
- かつ、その極値計算が要求されている
分数関数の問題の経験が多い人ならば分かると思いますが…
- 分数関数の微分=0ってキレイな値になることが多い
- 汚い場合は、「極値(最大・最小)をとる \(x\) の値を求めよ」って調整されることが多く、極値計算まで要求されることは少ない
ので、「安田の定理」を使ってメリットのあるケースはほとんどないです…



知ってると「検算でちょっと役立つかな」ってくらい(笑)
でもそれだと「安田の定理」で記事を作ってる意味がないので…
検索がかけやすく、比較的最新の2020~2022で、「安田の定理」を使ってメリットのある問題を必死に探しました!



「必死に」じゃないと見つからなかったです…
だから…繰り返すけど…覚えておく必要は全くない!
| 2020~2022で「安田の定理」を使ってメリットのある問題 | |
|---|---|
| 2021学習院大 | 三角関数からの分数関数 |
| 2021日本女子大 | 三角関数からの分数関数 |
| 2021長崎大 | 三角関数からの分数関数 |
| 2021東京理科大 | 軌跡からの分数関数 |
2021ばっかりですね(笑)ダブル・トリプルチェックしたわけではないので、見落としの可能性が多分にあることはご容赦くださいm(_ _)m
最後の問題はそこそこメリットがある問題だったので…
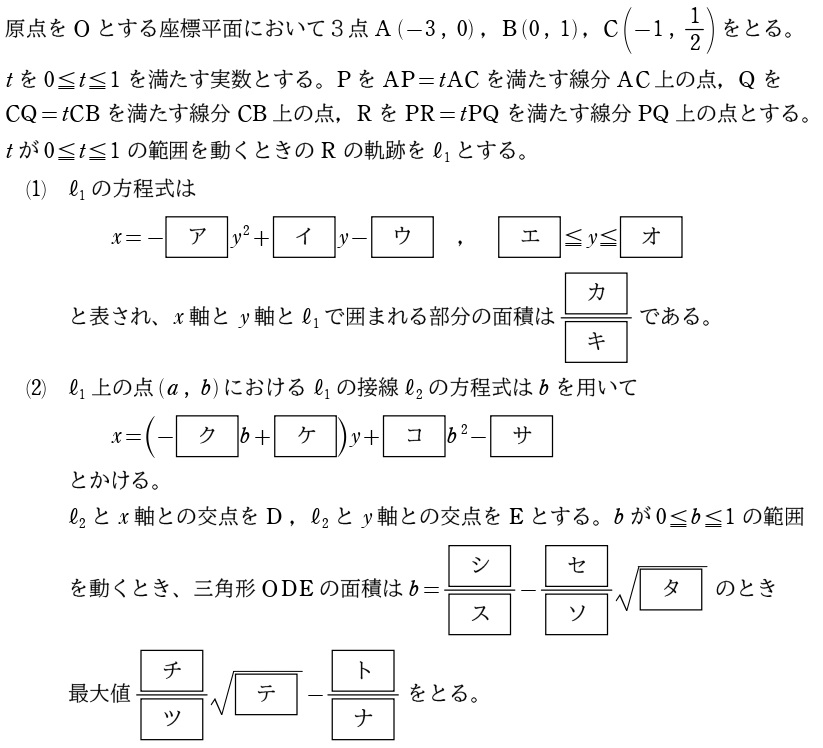
使用例(2021東京理科大)



出題学部と学科までは分かりませんでしたm(_ _)m
取りあえず20分くらいで解いてみてください↓
問題



- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
考え方
(1)はひたすらに内分点公式を使うだけ。これで \(\textrm{R}\:(x\:,\:y)\) を \(t\) の式で表せたら、\(t\) を消去して \(\ell_1\) の方程式が完成です。\(x\) が \(y\) の2次関数となるので、\(x\) 軸と \(y\) 軸との囲む面積は \(y\) 軸積分で求めましょう。
(2)の最初は逆関数に慣れてないとちょっとビックリしちゃうかもしれません。
\(y=f(x)\) の \(x=a\) における接線は、\(y=f'(a)(x-a)+f(a)\)
の \(x\) と \(y\) の入れ替えを意識し、
\(x=g(y)\) の \(y=b\) における接線は、\(x=g'(b)(y-b)+g(b)\)
とします。この \(x\) 切片と \(y\) 切片を求めて三角形ODEの面積を \(b\) で表すと、
分数関数 \(f(b)\) となり、\(f'(b)=0\) となる \(b\) が解の公式により汚くなる
という「安田の定理」が使えるケースの登場です。



解答では、
『「安田の定理」を使わない場合→使った場合』
の順で掲載しました!
共に次数下げを考えるのは変わりませんが、「安田の定理」を使うと、
- 分子の次数下げの計算が楽になる
- 分母を定数値にできるので、有理化の必要がなくなる
ということで、行数からも分かる通り、計算はかなり楽になります。



実際に僕は、「安田の定理」を使った打ち込みでは答が当たり、使わない打ち込みでは答を外しました(笑)
解答






まとめ
徹底的に解説してきた通り…



「安田の定理」を覚えておく必要は全くない!
です。偏差値65いってない人は、もっと他の重要定理を暗記しましょう!
でも…偏差値70を超えちゃうと…
- 安定的に偏差値70を超えるのが目標
- そのために計算ミスを減らす必要がある
- 結局、マイナーなテクニックの暗記が必要
になっちゃうんですよね…そ~ゆ~数学強者のためのテクニック、それが「偉い安田先生」=「安田亨先生」が発見した「安田の定理」です!
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。



「安田の定理」を暗記するか否かに関わらず…
君の大学受験が最高の結果になることを祈ってます!








