2025筑波大【数学】解説・解答・講評

2025筑波大学の数学の解説・解答・講評をお届けします！

全体的に考え方は外してないと思うんですが、確認役がいないため、最終的な値には全く自信がありません(笑)ミスや致命的な間違いを見つけた方は、X（Twitter）のDM等でご指摘頂けますと幸いですm(_ _)m

筑波大の数学の特殊性

筑波大の数学の入試では、
文系数学と理系数学が同じ冊子で配られる！

共通テスト↓

なんかと一緒です。ⅠＡの受験者にもⅠの問題が配られるのと同様。

2021～2025の筑波大数学

全体大問数	〔１〕～〔６〕の６問
文系数学で解く大問	〔１〕～〔３〕から２問選択
理系数学で解く大問	〔１〕～〔３〕から２問選択、 〔４〕～〔６〕から２問選択、 計４問を解答

因みに、解く問題数が理系の半分にも関わらず…文系にも理系と同じ試験時間120分が与えられるようです…

文系生徒であれば、〔１〕～〔３〕を全て解いて、少しでも完答に近づける２問を解答用紙に清書するのが良いと思います。

本記事では〔１〕～〔６〕全ての解説・解答を記載し、どの問題を選択するべきだったか等を講評にまとめます。

〔１〕

問題

考え方

(1)はただのヒントで、

\(a_1\:,\:a_2\) と \(a_2\:,\:a_3\) の関係式だけで、
全部の \(n\) で条件(A)が成立するようにしてあるよ～

ってことです。(1)を↓

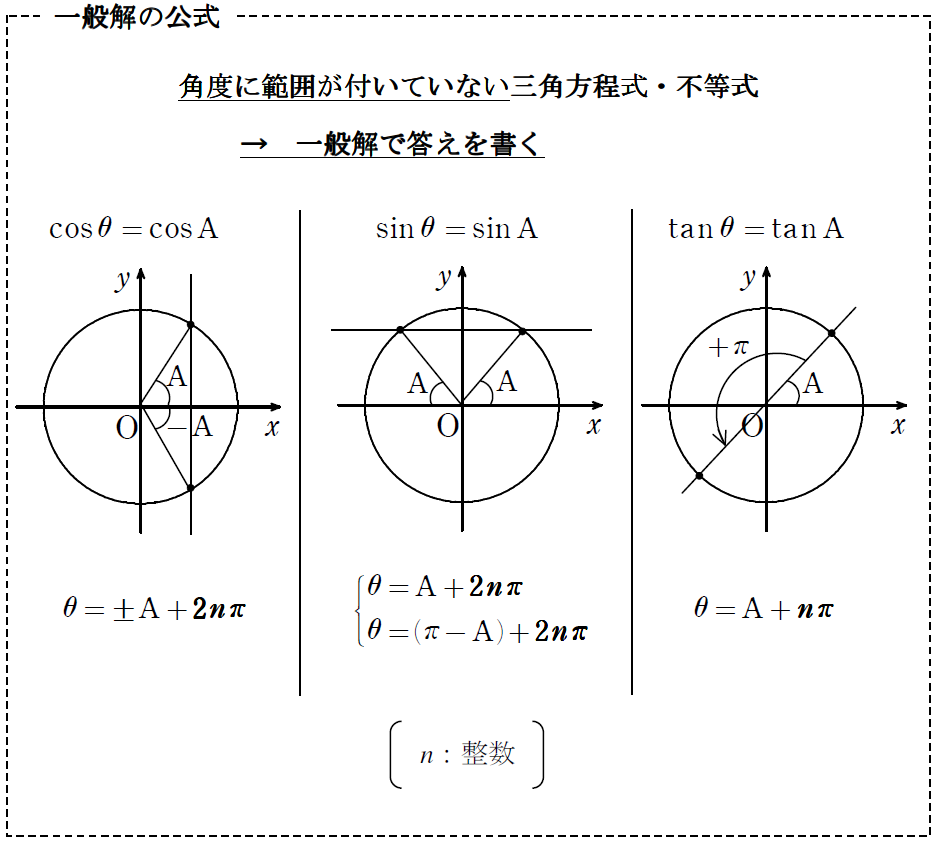
のtanバージョンで片付けたら、(2)と(3)は背理法での整数論証。(3)が正しく解ければ、(4)は整数問題における常套の、範囲の「絞り込み」（解答のように \(l\) の範囲を「絞り込み」するのが良いでしょう）を行うだけなので頭を悩ますことはありませんが…

繰り返しになりますが、絶対に選択してはいけない問題です。

解答

〔２〕

問題

考え方

(1)は「定数分離法」で、

\(f(x)=x^3-x+p=0\) がただ１つの実数解をもつ
↓
\(y=p\) と \(y=-x^3+x\) がただ１つの共有点をもつ

と言い換え、\(y=-x^3+x\) のグラフを描いて \(y=p\) のグラフを上下させるだけです。

(2)は↓

を使うのは明白でしょう。解と係数の関係で３等式を立式したら、\(a\:,\:c\:,\:p\) を \(b\) で表し、(1)の結果から \(b\) の範囲を求めるだけ。記述式なんで \(c\) のルートの中が０以上って条件（解答の⑤）もしっかり記述した方がいいと思います、結果には影響しませんが。

(3)は背理法からの整数論証ですが…ここで１つ鬼門が…

↑の結果が公式化されていないと、矛盾が導けないと思います…

解答

〔３〕

問題

考え方

思考的には何の山場もなく…

円の接線 \(\ell_1\:,\:\ell_2\) の方程式を \(a\) で表す
↓
(2)で与えられた面積比を線分比と捉えて \(a\) を確定
↓
(3)で \(\ell_1\:,\:\ell_2\) の傾きの積＝－１から90°を示し、直径に対する円周角の定理の逆

とするだけなんですが…

ソフトで作図するの面倒なので、\(\ell_1\:,\:\ell_2\) の方程式は式的に出しちゃいましたが、

中心と結んだ直線の傾きから、tanの２倍角の公式で
\(\ell_1\:,\:\ell_2\) の傾き \(m_1\:,\:m_2\) を出した方が楽

だと思います。でもそれでも計算はメンドウ…

文理問わず、この問題を完答した場合はかなり有利になったかと思います。

解答

〔４〕

問題

考え方

図形 \(C\) の方程式は「アポロニウスの円」の形ですが、(1)では「円であることを示し、」と言われているので、解答のように、

２乗して、円の方程式の一般形 \(az\overline{z}+\overline{\beta}z+\beta\overline{z}+c=0\) を導く
↓
因数分解により、円の方程式 \(|z-\alpha|=r\) を導く

とした方が良いでしょう。

\(z\) が円上、かつ変換の式が \(w=●z+\displaystyle\frac{▲}{z}\) の形のとき
↓
\(z\) を極形式でおく！

を用います。でも、\(z\) の偏角を \(\theta\) としてくれているので、かなり気づきやすいんじゃないでしょうか？(2)以降の鬼門としては、

(3)で絶対値の和が問われているので、(2)の結果は２乗の形になる

ことを意識できるかです。\(\sqrt{●^2}=|●|\) ですが、(3)で相加相乗平均の不等式から絶対値を外せるナイス作問。

カンタンな問題ではありませんが、典型ではあるので、なるべく完答して欲しい問題。

解答

〔５〕

問題

考え方

(3)の式の見た目の凶悪さに反して…

(1)は微分するだけ
↓
(2)は \(f(x)\) の \(e^{2(n-1)\pi}<x<e^{2n\pi}\) における増減表を作るだけ
↓
(3)は無限等比級数の和の公式を使うだけ

なので。ただ…

• (2)は抽象値 \(n\) が入ってるからそこそこ混乱する
• 同じ流れで(3)も混乱する
• 全体的に計算メンドウ…

計算ミスしたときのために、(3)の無限等比級数の和の公式を利用するところとかで公比の収束条件を丁寧に記述し、部分点は拾える解答にしましょう。

解答

〔６〕

問題

考え方

(1)は \(f(x)\) の増減表作るだけ
↓
(2)は積分区間 \(0≦x≦5\) から前者の不等式を証明し、
そこにインテグラルをくっつけて後者の不等式を証明するだけ
↓
(3)は \(V(t)\) を \(t\) の２次関数として立式し、その最小値を \(\alpha\) で表すだけ

でも解答の(3)の場合分けとか必要なのかな～とか色々アタマを悩ませちゃう問題。

2023や2024もそうだったんですが、やはり筑波大理系数学では〔６〕は選択しちゃいけないな、と再確認する問題でした。

解答

講評

2024の解説記事↓

も作成しましたが、これと比べると…

でしょう。特に文理共通範囲（ⅠＡⅡＢとＣのベクトル）の〔１〕～〔３〕がかなり難化した印象です。

• 〔１〕は今年の問題の中で一番難しい
• 〔３〕は計算量がメンドウ
• 〔２〕もそこまでカンタンではない

ので。また、理系専用範囲（ⅢとＣのベクトル以外）の〔４〕～〔６〕も、例年より難し目（ってか見た目がムズく見える）だったと思います。

冒頭で述べた通り、筑波大数学では文系も理系も解く問題を選べるわけですが、一般目線で言うと2025は…

大問番号	出題範囲	解くべき問題
〔１〕～〔３〕	文理共通範囲	〔２〕・〔３〕
〔４〕～〔６〕	理系専用範囲	〔４〕・〔５〕

でしょう。

文理問わず、〔１〕を選択しないことが大事！

なテストだったかと思います。可哀想なことに…

この難易度でも、医学部医学科だと３完／４は必要

になるでしょう…お医者さんになるってホントに大変…

今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ！

君の大学受験が最高の結果になることを祈ってます！