2025早稲田人科【数学選抜】解答速報

2025早稲田大学人間科学部の数学選抜の数学の解答速報をお届けします!
 めぐろ塾の安田
めぐろ塾の安田人員不足のため、一人で孤独にやっております(笑)
ミスを見つけた方は、X(Twitter)のDM等でご指摘頂けますと幸いですm(_ _)m
【問1】(必須問題)
問題


考え方



いつも通り小問集合。いつも通りカンタンです。
(1)の(a)は、袋の中の玉の総数をシグマ計算で求めて分母にするだけ。分子は \(k\) です。
(1)の(b)は余事象を利用しましょう。書かれた数字が同じになる確率をシグマ計算で求め、1から引くだけ。
(2)は典型的な逆像法の問題。めぐろ塾↓


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
では、
独立2変数関数の最大・最小
↓
\(=k\) とおいて、「共有点を持つ」と言い換え
ってキーワード化する内容です。(a)では、2円が内接状態になるときの半径の最大値を考えるだけ。(b)では、円と直線が接するときを考えるのでヘッセの公式を使うだけ。
全体的に計算量も少なく、完答はマストな問題です。



何と僕は(2)を両方とも計算ミスっておりました(笑)ご指摘頂いた方に厚く御礼申し上げますm(_ _)m
僕のようにはなりたくない問題です(笑)
解答




【問2】(必須問題)
問題


考え方



例年通り…【問2】は苦しんだ生徒が多いと思います…
上の式から、\(〇^2+△^2+▢^2≧0\) が作れることに気づく
↓
\(〇=0\:,\:△=0\:,\:▢=0\) とできるかが全て
の問題です。
- 等式2本だと「不定方程式」になるから、「連立方程式」と言われている以上、どちらかの等式から複数の等式が得られるはず
- 「実数 \(x\:,\:y\:,\:z\) を求めよ」と言われている
ことから、同様の問題の経験がある人は気づきやすい問題なんですが、そこまで頻出とは言えないので受験者の出来は悪そうです。



2020周辺の文系MACRHで結構使った記憶があります。
この【問2】を解けた人は、かなりアドバンテージが得られるでしょう。
解答


【問3】(必須問題)
問題


考え方
この記事↓


の「特徴的な出題」で提示している内容です。今年も出題してきやがりました。
(1)は余弦定理を与式の \(a^2\) に使うだけですが、辺のみの式に角度を登場させるので、意外と解けなかった人は多そう。
(2)は解答では、
(1)の \(A=120^\circ\) から、不等式の \(B+C=60^\circ\) とする
↓
不等式を変形し、\(bc≧1\) を導く
↓
等式と正弦定理から \(bc\) を \(B\) の三角関数で表し、最大値を求める
としました。この記事を見た受験生の方から、
最大値は、高さが外接円の中心を通るときで良くないですか?



って言われたんですが、不等式から出る \(bc≧1\) って条件が図的に視認しにくい、かつ底辺も動くので、全部式で完結しときました…大変でした(笑)
多分高さが外接円の中心通るときを考えても結果は一致すると思います。最後まで答が当たってれば大成功な問題でしょう。
解答




【問4】(選択問題)
問題


考え方
文系生徒用の選択問題です。【問5】は理系の数学Ⅲからの出題なので。
(1)は、「三角形の内接円の半径は、面積を使って求める」ってのが定型化されている人であれば、
「四面体の内接球の半径は、体積を使って求める」
ってことに気づけるでしょう。



2017の早稲田理工でも出題されている処理で、ここまではムズくないんですが…(2)・(3)は僕も初見の問題でした…
空間での鉄則は、「断面を抜き出して考える」です、無理に立体をイメージしないことが大切!
これで(2)はカンタンに片付くんですが…(3)は4球の中心が四面体をなすってことから考えないと厳しいので…かなりムズいです。



僕も(3)だけで30分近く使っちゃいました…
興味あって調べたら、youtubeに同様の問題載せてる人がいて、結果は一致したんで多分答は大丈夫かと…
(1)は確保したい、(2)まで解けてれば大成功、な問題でしょう。
解答






【問5】(選択問題)
問題


考え方
理系専用範囲の数Ⅲからの出題です。



理系の人は【問4】より絶対こっちを選択した方が良かったでしょう。
(1)は増減表作るだけ。因みに結果は、
\[\displaystyle\frac{a^{-\frac{1}{\log a}}}{\log a}=\displaystyle\frac{a^{-\frac{\log_{a}e}{\log_{a}a}}}{\log a}=\displaystyle\frac{a^{\log_{a}e^{-1}}}{\log a}=\displaystyle\frac{1}{e\log a}\]
と書けるみたいですね。受験生の方に教えて頂きました。僕、当日気づけなかったです(笑)
(2)は、これ↓
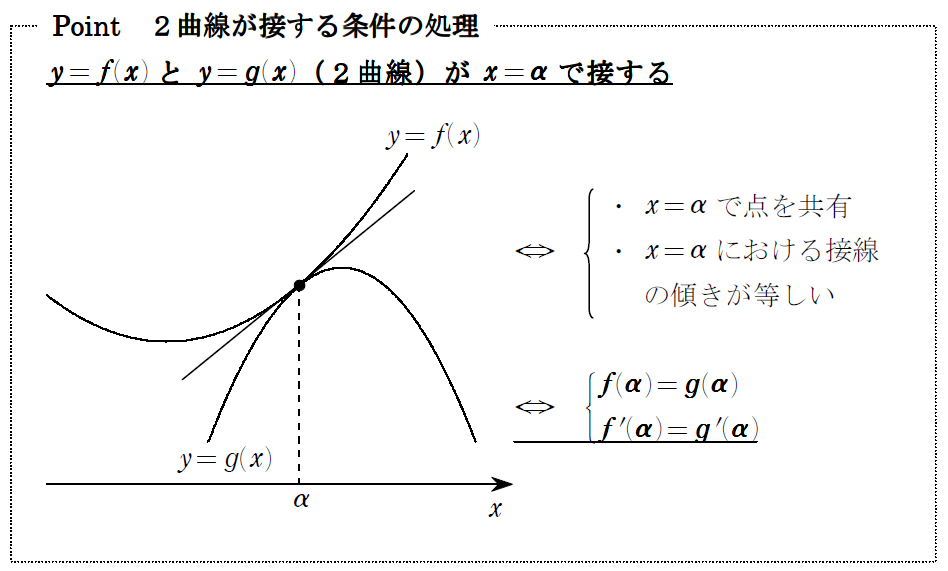

使っとくのがいいでしょう。今回は片方が直線 \(y=x\) ですが、問題なく使えます。
(3)は、「2つの共有点を持つ」=「連立した方程式が2つの実数解を持つ」と考えるのは当然とし、
\(a^x\) と \(\log_{a}x\) の混在する方程式は解析しづらい
↓
\(y=a^x\) と \(y=\log_{a}x\) が逆関数で、\(y=x\) 対称
↓
「\(y=a^x\) と \(y=\log_{a}x\) の交点」=「\(y=a^x\) と \(y=x\) の交点」
と考えますが、\(y=x\) が(2)で登場しているので、気づきやすくはあるでしょう。因みにこの交点の変換は、単調増加な関数でしか使えないので、解答では一応断ってますが…



減点される可能性は低いと思います。仮に減点されても、答当たってれば大成功な問題でしょう。
解答




講評
昨年も解答速報↓


を行いましたが、これと比べると…
| 解答方式 | 試験時間 | 大問数 | 難易度 |
|---|---|---|---|
| 記述式 | 120分 | 5問 (【問4・5】は、どちらかを選択して解答。文系は【問4】を選択するしかない) | やや難化 |
に思えます。
- 【問2】はかなり類問の経験が必要
- 【問3】がかなり解きにくい
- 【問4】はかなりムズい
ので。特に【問4】を選択するしかない文系生徒が不利な構成だったと思います。



ま~でも…
2022~2024の合格最低点は、6割程度です。
文系生徒でも、
1を完答、2・3のどちらかを完答!
していれば、プラス部分点で充分戦える試験だったでしょう。
今回の記事に関しての質問や、ミスを見つけた場合のクレーム(笑)めぐろ塾へのお問い合わせはこちら↓からお気軽にどうぞ!


- 日本全国どこからでも受講可能!
- 完全個別指導コースあり(オンラインも可)!
- 初回面談・初回授業は完全個別で無料(オンラインも可)!



初回面談は全て私めが個別に対応させて頂きますm(_ _)m
お気軽にお問い合わせください↓
電話番号からのお問い合わせの場合、授業や面接中で対応できない場合は折り返しご連絡させて頂きますので、留守番電話にご用件を残しておいて頂けると助かります(セールス・勧誘のお電話は固くお断り致します)。
頂いたお問い合わせへのリアクション以外で、こちらからご連絡することは一切ありません。安心してお問い合わせください。
君の大学受験が最高の結果になることを祈ってます!








